| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- Region Proposal Networks
- GAN
- Fast R-CNN
- 군집화
- 군집
- Clustering
- 적대적 생성 신경망
- hierarchical clustering
- Deep Learning
- K-means
- 비지도학습
- 이미지 초해상화
- Faster R-CNN
- RPN
- super-resolution
- SRGAN
- CV
- Object Detection
- Today
- Total
수혁지능
[Practical Statistics for Data Scientists] Tree Models 본문
트리 모델
트리 모델은 CART(classification and regression tree), 의사결정트리(decision tree), 트리(tree)라고 불리며, 효과적이고 대중적인 분류 및 회귀 방법이다. 여러 가지 규칙을 순차적으로 적용하면서 독립 변수 공간을 분할하는 분류 모형이라고 할 수 있다.
즉, 트리 모델은 if-then-else 규칙의 집합체이며 이해하기도 쉽고 구현하기도 쉽다. 선형회귀나 로지스틱 회귀와 반대로 트리는 데이터에 존재하는 복잡한 상호관계에 따른 패턴들을 발견하는 능력이 있다. KNN이나 나이브 베이즈 모델과는 달리, 예측변수(X)들 사이의 관계로 단순 트리 모델을 표시할 수 있고 쉽게 해석도 가능하다.
간단한 예제 코드
저번 주차에 사용했던 loan3000 데이터를 이용하여 예측변수를 borrower_score, payment_inc_ratio로 두고 default(연체) 혹은 paid off(상환)여부에 대해 알아보자.(Classification problem)
일단 tree model을 사용하기 위해 sklearn.tree를 이용해 필요한 library를 Import한다.

이제 DecisionTreeClassifier를 모델로 하여 X,y를 fit시킨다. 각 분할 영역의 동질성을 측정하는 기준은 entropy를 사용한다.(추후에 설명). min_impurity_decrease는 트리 분할을 하는데 필요한 최소 불순도 감소량으로서 추후에 설명한다.
fitting된 모델을 plot으로 그리면 다음과 같은 트리 모델이 만들어진다.

그림을 그릴 때는 실제 나무구조와는 반대인, 뿌리가 위로 가고 잎 부분이 아래로 가는 모습을 띈다. 맨 위의 노드를 루트 노드라 하고 마지막 가지에 있는 트리 노드를 잎 노드라고 한다. 해당 노드가 참이면 왼쪽으로 움직이고, 거짓이면 오른쪽으로 움직이면서 계층구조의 트리를 통과하여 분류 규칙이 결정된다.
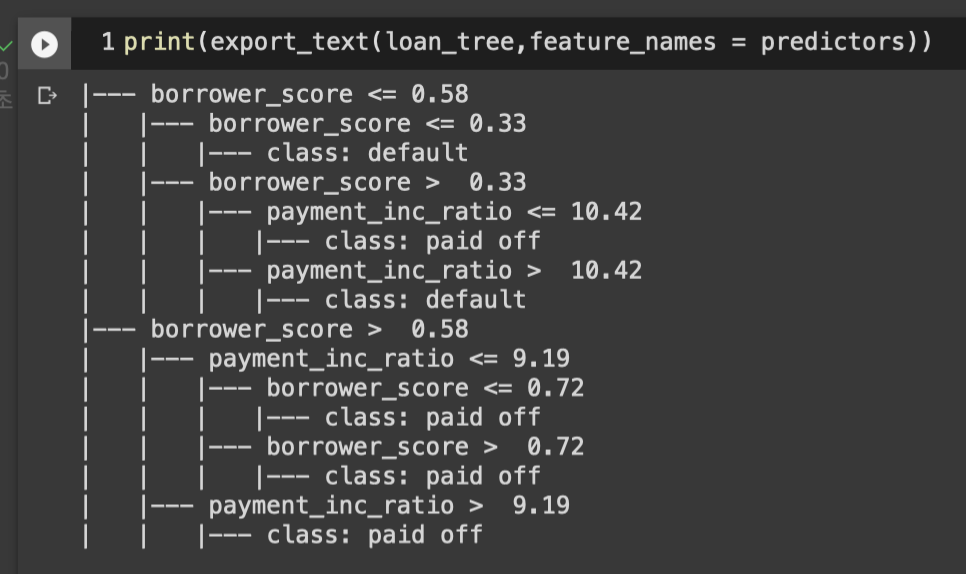
만약 borrow_score가 0.6이고 payment_inc_ratio가 8.0인 대출 정보를 얻었다면, 이 모델의 규칙을 따라 루트 노드에서 오른쪽으로 이동하여 paid off class로 분류가 되는 것을 알 수 있을 것이다.
export_text module을 사용하면 text 구조로도 tree 모델을 아래와 같이 나타낼 수 있다.
트리 모델의 재귀 분할 알고리즘
의사 결정 트리를 만들 때는 재귀 분할이라고 하는 알고리즘을 사용한다. 예측변수 값을 기준으로 데이터를 반복적으로 분할해나가는 과정으로, 분할할 때는 상대적으로 같은 클래스의 데이터들끼리 구분되도록 한다.
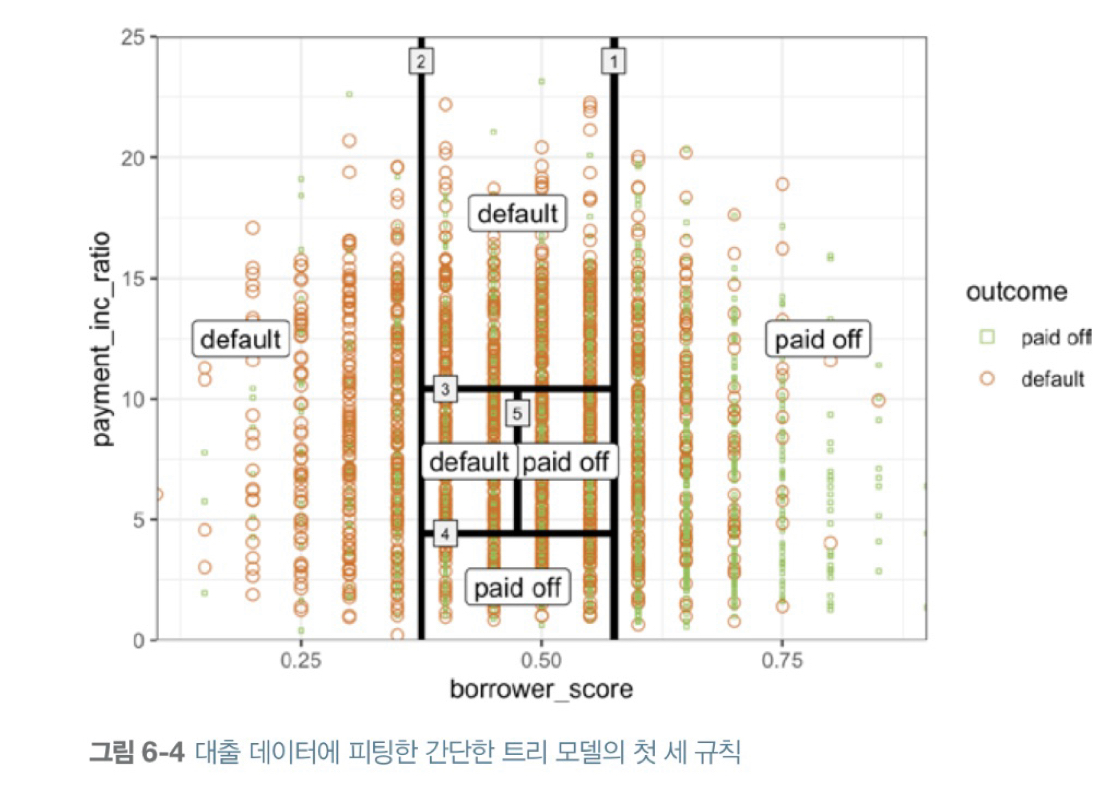
아래는 트리를 통해 만들어진 분할 영역을 보여준다. 아래 실선의 번호가 그림을 분할하는 순서이다.
재귀적 분할 방법을 글로 표현하면 다음과 같다.(응답변수 Y, P개의 예측변수 집합 Xj(j=1,..,p), 파티션 A)
<분할 알고리즘>
1. 각 예측변수 Xj에 대해
a. Xj에 해당하는 각 변수 sj에 대해
- A에 해당하는 모든 레코드를 Xj < sj인 부분과 나머지 Xj >= sj인 부분으로 나눈다.
- A의 각 하위 분할 영역 안에 해당 클래스의 동질성을 측정한다.
b. 하위 분할 영역 내에서의 클래스 동질성이 가장 큰 sj값을 선택한다.
2. 클래스 동질성이 가장 큰 변수 Xj와 sj값을 선택한다.
<재귀 알고리즘>
1. 전체 데이터를 가지고 A를 초기화
2. A를 두 부분 A1, A2로 나누기 위해 분할 알고리즘을 적용
3. A1, A2 각각에서 2번 과정을 반복
4. 분할을 해도 더는 하위 분할 영역의 동질성 개선되지 않을 정도로 충분히 분할 진행했을 때, 알고리즘 종료.
알고리즘의 최종 결과는 위 그림과 같은 데이터 분할 영역이고, 해당 영역에 속한 Y들의 다수결 결과에 따라 0 or 1로 예측이 결정된다.
또한, 분할 영역에 존재하는 0과 1의 개수에 따라 확률값을 구할 수도 있다.
ex) P(Y=1) = 파티션 내 1의 개수 / 파티션의 크기(영역에 속한 전체 데이터의 개수)
동질성과 불순도 측정하기
앞의 재귀 분할 알고리즘을 적용하기 위해선 각 분할 영역에 대한 동질성, 즉 클래스 순도나 불순도를 측정해야 한다.
해당 파티션 내 오분류된 레코드의 비율 p를 이용해 예측의 정확도를 표시할 수 있으며 p는 0(완전)~0.5(순수 랜덤추측) 사이의 값이다.
그러나 정확도보다는 지니 불순도와 엔트로피를 대표적인 불순도 측정 지표로 사용한다.
<지니 불순도>
I(A) = p(1-p)
<엔트로피>
I(A) = -plog2(p)-(1-p)log2(1-p)
p에 따른 정확도, 지니 불순도, 엔트로피의 개형은 다음과 같다.
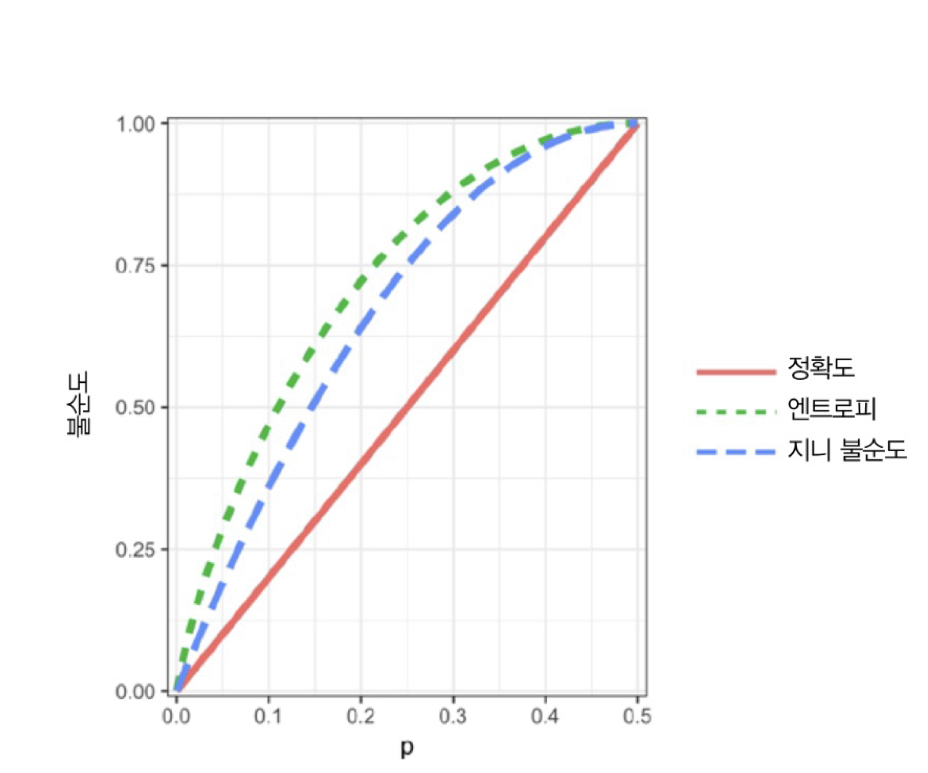
앞의 분할 알고리즘도 분할로 만들어지는 각 영역에 대해 불순도를 측정한 다음, 가중평균을 계산하고 단계마다 가장 낮은 가중평균을 보이는 분할 영역을 선택했다.
트리 형성 중지와 복잡도 제어
트리가 커질수록 분할 규칙들은 세분화되고, 믿을 만한 관계들을 확인하는 '큰' 규칙에서 노이즈까지 반영하는 '작은' 규칙을 만드는 단계로 변화한다. 이는 Overfitting과도 연관된 중요한 문제로 어느 정도 적당한 크기에서 트리 형성을 중지하는 것이 반드시 필요하다. 학습 데이터의 노이즈까지 학습해버리면 새로운 데이터를 분류할 때 방해가 되기 때문이다.
파이썬에서는 여러 가지 방식을 이용해 트리 형성을 제어한다.
1. DecisionTreeClassifier의 parameter인 min_samples_split(노드 분할 시 필요한 최소 sample 수)과 min_samples_leaf(잎 노드가 되기 위한 최소 sample 수)를 사용하여 분할을 제어한다. 즉, 분할을 통해 얻어지는 잎의 크기가 너무 작다면 분할을 멈춘다.
2. min_impurity_decrease(분할에 필요한 최소 불순도 감소량)을 이용해 분할을 제어한다. 즉, 새로운 분할 영역이 '유의미'한 정도로 불순도를 줄이지 않는다면 굳이 분할하지 않는다.
3. sklearn의 cpp_alpha를 이용해 트리 가지치기를 실행한다. 값이 커질수록, 가지치기를 많이 진행한다.(트리는 작아진다) max_depth(트리 최대 깊이)를 이용해 트리 복잡도를 제어할 수 있다.
4. GridSearchCV를 사용하여 1~3의 모든 parameter들의 최적의 값을 찾는다.
트리 모델을 통한 예측과 활용
앞에선 트리 모델을 통한 Classification을 계속 다뤘지만 regression도 충분히 가능하다. 동일한 재귀 분할 알고리즘을 통해 하위 영역을 만들어낸다. 다만 각 하위 분할 영역에서 평균으로부터의 편차들을 제곱한 값을 이용해 불순도를 측정한다는 점, RMSE를 이용해 예측 성능을 평가한다는 점에 차이가 있다. 모듈은 sklearn.tree.DecisionTreeRegressor를 사용한다.
종합적으로 트리 모델을 통해 예측을 진행하게 되면, 어떤 변수가 중요하고 변수 간에 어떠한 관계가 있는지를 잘 보여줄 수 있다. 기존의 '블랙박스'와 같은 모델의 한계를 넘어 예측변수들 간의 비선형 관계를 잘 나타낼 수 있다.
또한, 트리 모델은 if-then으로 이어진 규칙들의 집합이어서 매우 직관적이고 간단하므로, 비전문가들과 커뮤니케이션을 할 때도 아주 효과적이라고 할 수 있다.
그러나 보통 예측을 진행할때는 성능상의 이유로 단일 트리보다는 다중 트리나 앙상블 기법인 랜덤 포레스트와 부스팅 트리 알고리즘을 사용하는데, 이 때는 명확한 규칙들의 연속 등의 전달 능력은 잃어버린다는 단점이 존재한다.




