| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- Region Proposal Networks
- RPN
- 군집화
- K-means
- Object Detection
- Clustering
- hierarchical clustering
- 적대적 생성 신경망
- Fast R-CNN
- super-resolution
- 이미지 초해상화
- CV
- GAN
- 군집
- 비지도학습
- SRGAN
- Deep Learning
- Faster R-CNN
- Today
- Total
수혁지능
[Practical Statistics for Data Scientists] Naive Bayes Classification & Discriminant Analysis 본문
[Practical Statistics for Data Scientists] Naive Bayes Classification & Discriminant Analysis
혁수 2023. 1. 3. 01:39사전지식
두 확률 변수 A,B 의 조건부확률,사전 확률,사후 확률에 대해 알아보고 베이즈 정리에 대해 살펴보자.
여기서 P(A|B)라는 조건부확률은 사건 B가 일어난 후 사건 A가 일어난 확률이다. 여기서 사건 B는 먼저 일어난 일이므로 Before라 정의하고 사건 A는 나중에 일어난 일이므로 After라고 정의한다.

조건부확률
P(B)는 사건 A가 발생하기 전 사건 B가 일어난 확률이므로 사전 확률이라 할 수 있고, P(B|A)는 사건 A가 일어났을 때 사건 B가 앞서 일어났을 확률이므로 사후 확률이라고 할 수 있다.
이 확률들은 아래 그림과 같이 '베이즈 정리'로 묶일 수 있다.

베이즈 정리
나이브 베이즈
나이브 베이브 알고리즘은 주어진 결과에 대해 예측변숫값을 관찰할 확률을 사용하여, 예측변수가 주어졌을 때, 결과 Y=i를 관찰할 확률, 즉 정말 관심 있는 것을 추정하는 알고리즘이다.
완전한 베이즈 분류 >> 표본에서 새로 들어온 레코드와 정확히 일치하는 데이터를 찾는다!
1. 예측변수 값이 동일한 모든 레코드들을 찾는다
2.해당 레코드들이 가장 많이 속한 클래스를 정한다.
3.새 레코드에 해당 클래스를 지정한다.
BUT 예측변수의 개수가 일정 정도 커지면, 데이터들이 서로 완전히 일치하는 경우 거의 X >> 완전한 베이즈 분류는 현실적이지 않다.
대안: 나이브 베이즈 분류
1. 이진 응답(Y=0 or Y=1)에 대해, 각 예측변수에 대한 조건부확률 P(Xj | Y=i)를 구한다. 훈련데이터에서 Y=i인 레코드 중 Xj값의 비율로 구한다.
2. 각 확률값을 모두 곱한다음, Y=i에 속한 레코드들의 비율(P(Y=i))을 곱한다.
3. 모든 클래스에 대해 1~2단계 반복
4. 클래스 i의 확률을 2단계에서 모든 클래스에 대해 구한 확률값을 모두 더한 값으로 나누면 결과 i의 확률을 구할 수 있다.
4. 이 예측변수에 대해 가장 높은 확률을 갖는 클래스를 해당 레코드에 할당한다.
이 알고리즘은 예측변수 X1,X2,...,Xp가 주어졌을 때의 출력 Y=i의 확률에 대한 방정식으로 표현될 수 있다.
P(Y=i | X1,X2,X3,...Xp)
기존의 정확한 베이즈 분류에서는 아래와 같이 식을 작성할 수 있다.
P(Y=i | X1,X2,X3,...Xp) = P(Y=i)P(X1,...,Xp|Y=i) / P(Y=0)P(X1,...,Xp|Y=0) + P(Y=1)P(X1,...,Xp|Y=1)
나이브 베이즈는 조건부 독립성을 가정(Xj가 k!=j인 모든 XK와 서로 독립이라고 가정)하므로 이 방정식을 다음과 같이 전개한다.
P(Y=i | X1,X2,X3,...Xp) = P(Y=i)P(X1|Y=i)P(X2|Y=i)...P(Xp|Y=i) / P(Y=0)P(X1,...,Xp|Y=0) + P(Y=1)P(X1,...,Xp|Y=1)
모든 예측변수가 동일해야했던 정확한 베이즈 분류의 한계를 극복하고 각 조건부 확률 P(Xj|Y=i)의 곱으로 예측변수 벡터의 정확한 조건부확률을 충분히 잘 추정할 수 있다라는 것을 보여준다.
좀 더 간단화하면 아래 그림처럼 수식화할 수 있다.
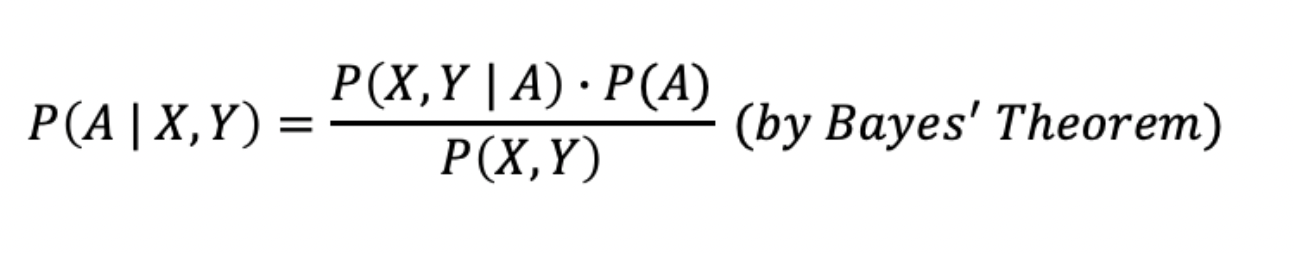
결합확률과 베이즈 정리
여기서 X,Y는 독립적인 데이터의 특징이며 A는 전체 클래스 혹은 레이블 중 하나라고 할 수 있다.
실습코드
파이썬의 sklearn 라이브러리를 활용하여 손쉽게 나이브 베이지 분류기를 실습해볼 수 있다.
예측변수와 결과변수를 구분하고, 모델을 피팅하기 전 범주형 변수들을 one_hot_encoding을 통해 수치형으로 변환한 후 sklearn.naive_bayes.MultinomialNB 모델에 피팅한다.
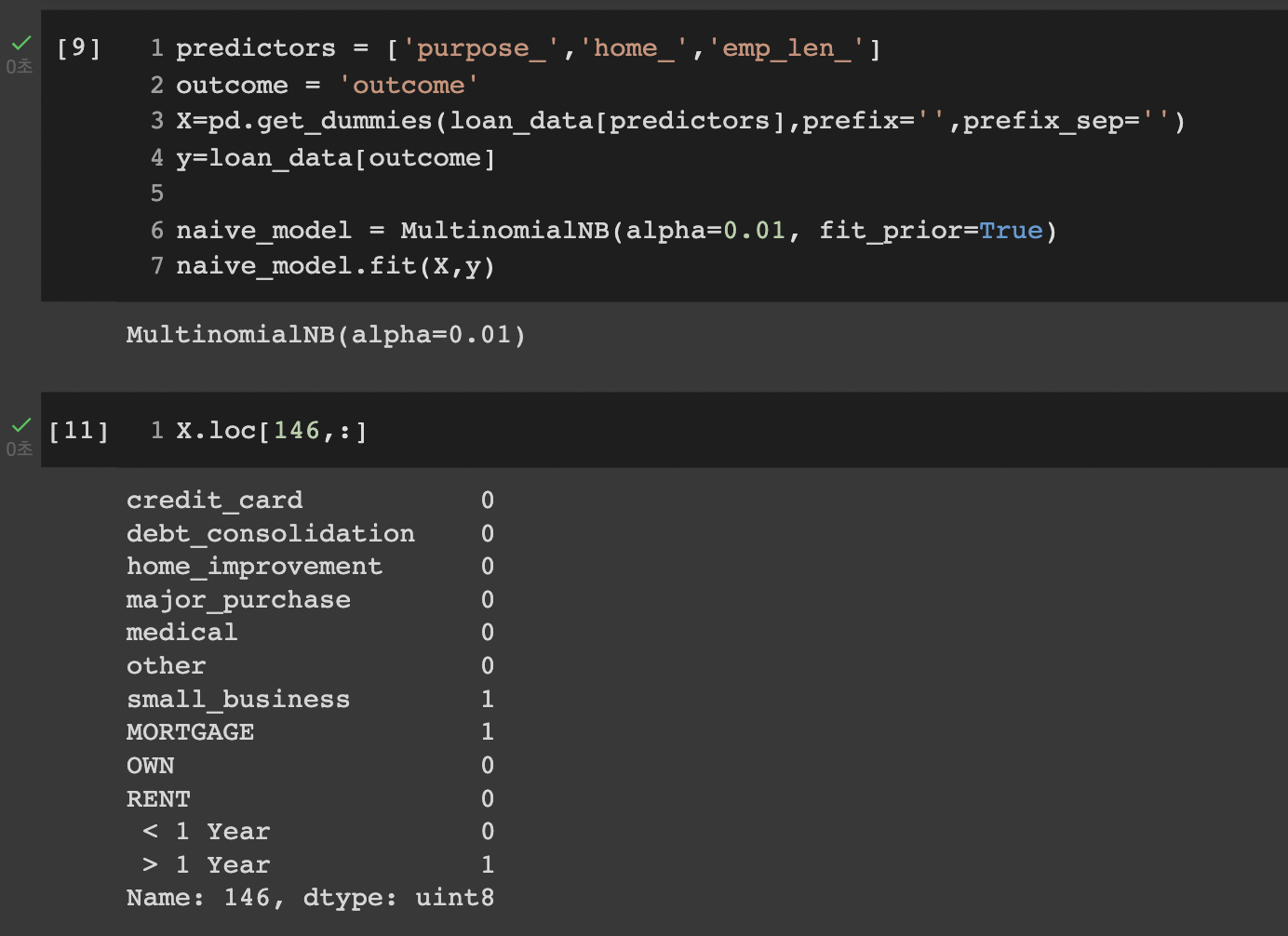
실제 실습코드와 예측변수를 더미화(pd.get_dummies)한 모습
훈련된 MultinomialNB 모델에 X의 특정 행을 input으로 넣으면 class가 확률과 함께 predict 되어 반환된다.
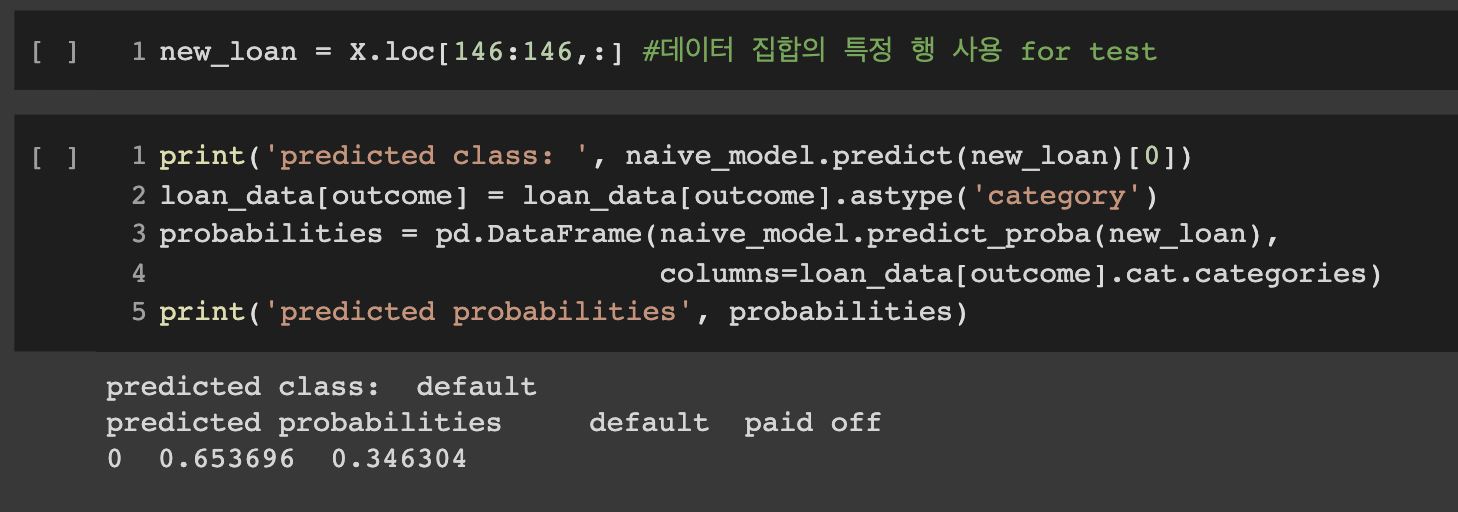
default: 0.653696, paid off: 0.346304로 class가 default로 예측된 모습
수치형 예측변수에서의 나이브 베이즈 분류기
일반적으로 베이즈 분류기는 예측변수들이 범주형인 경우에 적합!
ex) 스팸 메일 분류에서 특정 단어, 어구, 문자열의 존재 여부 등
수치형 변수에 나이브 베이즈를 적용하려면 2가지 방식 중 1개를 택해야한다.
1. 수치형 예측변수를 비닝(binning)하여 범주형으로 변환한 뒤, 알고리즘을 적용한다.
2. 조건부확률 P(Xj | Y=i)를 추정하기 위해 정규분포와 같은 확률모형을 사용한다.
판별분석
판별 분석은 두 개 이상의 모 집단에서 추출된 표본들이 지니고 있는 정보를 이용하여 이 표본들이 어느 모집단에서 추출된 것인지를 결정해 줄 수 있는 기준을 찾는 분석법이다.
LDA(선형판별분석)
LDA는 데이터 분포를 학습하여 결정경계(Decision boundary)를 만들어 데이터를 분류(classification)하는 모델이다.
LDA는 아래 그림처럼 데이터를 특정한 축에 사영(Projection)한 후 두 범주를 잘 구분할 수 있는 직선을 찾는 것이 목표입니다.
두 범주를 잘 구분할 수 있는 직선은 사영 후 두 범주의 중심(평균)이 서로 멀도록, 그 분산은 작도록 해야한다.
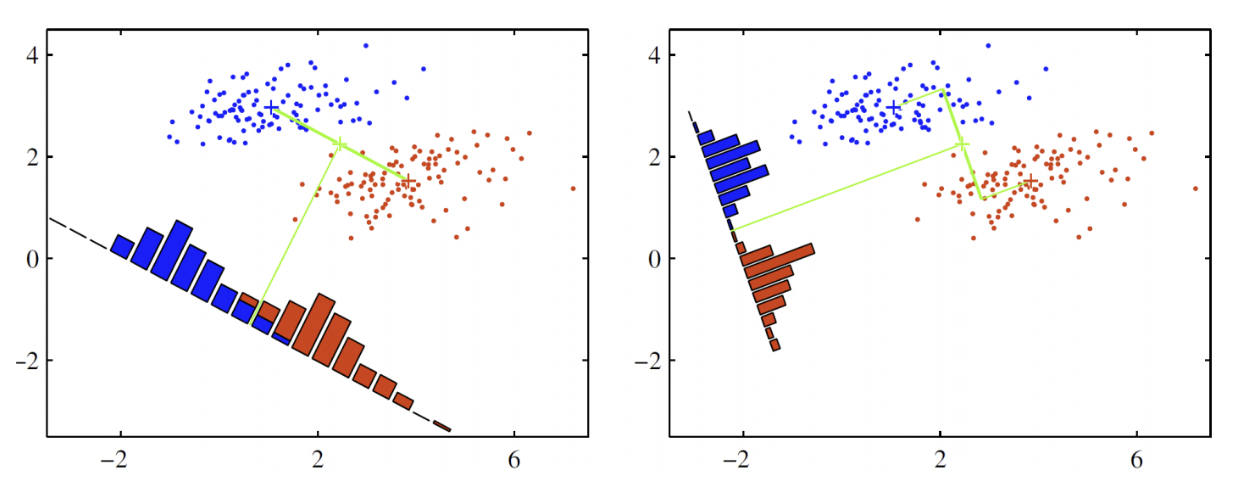
오른쪽 그림이 왼쪽 그림보다 LDA가 잘 되었다고 할 수 있다.
피셔의 선형판별과 공분산행렬
LDA의 본질적인 원리는 피셔가 제안했던 선형판별과 같다.
피셔의 선형판별은 두 개의 연속형 변수 (x,z)를 사용하여 이진 결과변수 y를 예측하려는 분류 문제에서 시작한다.
보통 예측변수가 정규분포를 따르는 연속적인 변수라는 가정이 있지만, 실제로 그렇지 않아도 잘 동작한다.
피셔의 선형판별은 그룹 안의 편차와 다른 그룹간의 편차를 구분하는데, LDA는 '내부' 제곱합 SS내부에 대한 '사이' 제곱합 SS사이의 비율을 최대화하는 것이 목표이다. 두 그룹은 y=0에 대해 (x0,z0), y=1에 대해 (x1,z1)으로 나뉘게 된다.
이 방법은 SS사이/SS내부를 최대화하는 선형결합 Wx*x + Wz*z를 찾는다. 사이 제곱합의 각 값은 두 그룹 평균 사이의 거리 제곱을 말하며, 내부 제곱합은 공분산행렬에 의해 가중치가 적용된, 각 그룹 내의 평균을 주변으로 퍼져 있는 정도를 나타낸다.
여기서 공분산이라는 개념을 이해하고 가야하는데, 공분산은 두 변수 x와 z사이의 관계를 의미하는 지표이다. xbar와 zbar는 각 변수의 평균을 나타낸다. x와 z사이의 공분산 Sx,z는 다음과 같다. 여기서 n은 레코드의 개수를 의미하고 분모로는 n이 아닌 자유도인 n-1이 들어갔음을 알 수 있다.
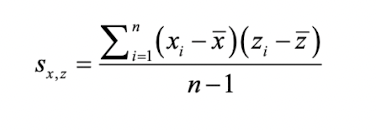
공분산 Sx,z
다른 수식으로는 아래와 같이 나타낼 수도 있다.
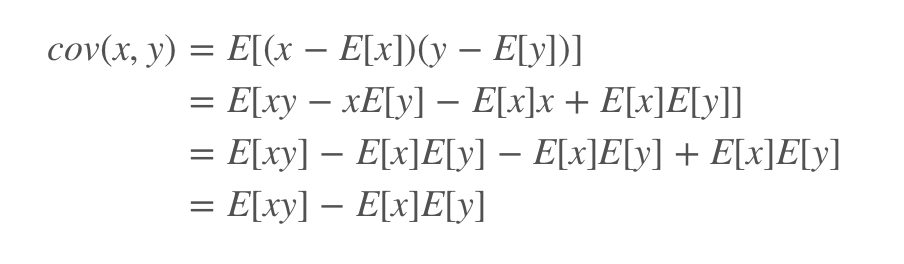
상관계수와 마찬가지로 공분산이 양수면 양의 관계이고, 두 변수의 변화경향성이 유사하다는 것을 알려준다.
공분산이 음수면 음의 관계이고, 두 변수의 변화경향성이 반대이다.
공분산행렬은 변수들 사이의 공분산을 행렬 형태로 나타낸 것으로서, 정방행렬(Square matrix)이자 transpose를 시켰을 때, 동일한 행렬이 나타나는 대칭행렬(Symmetric matrix)이다. 형태는 아래 사진과 같다.
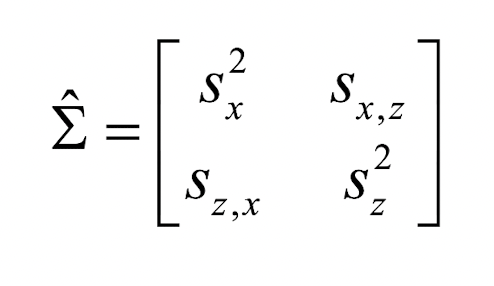
각 변수의 분산: 대각원소, 변수들 사이의 공분산: 비대각원소
최종적으로 LDA는 사이 제곱합을 최대화하고 내부 제곱합을 최소화하여 두 그룹 사이를 가장 명확하게 나누는 방법이라고 할 수 있다.
실습코드
실습 코드는 다음과 같다. 두 예측변수 borrow_score와 payment_inc_ratio를 이용해 대출 데이터 표본에 LDA를 적용하고 선형판별자 가중치를 구한다.
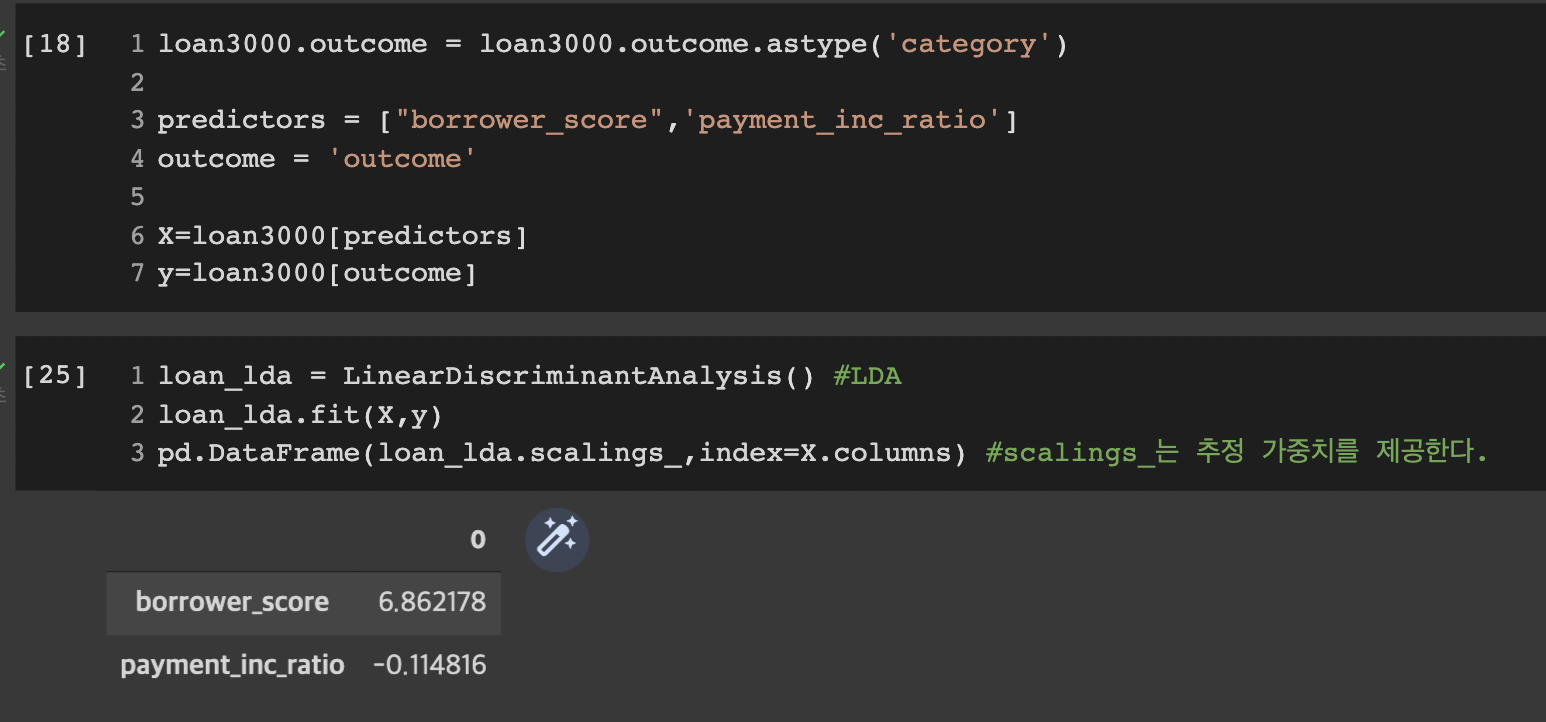
먼저 예측변수와 결과변수를 정의하고 LDA 모델을 학습시킨다. scalings_property를 이용해 추정 가중치를 확인한다.
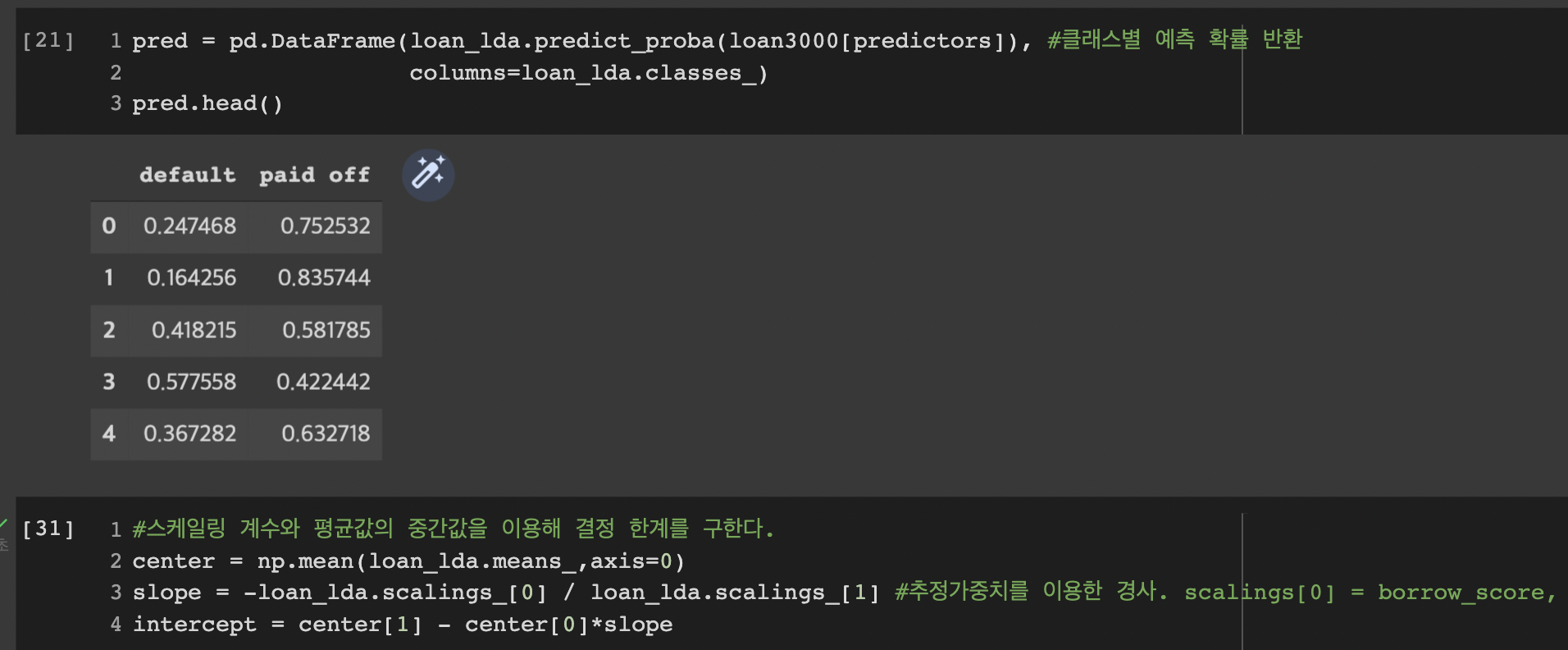
피팅된 모델에서 predict_proba메서드를 이용해 default(연체) 혹은 paid off(상환)에 대한 확률을 반환한다.
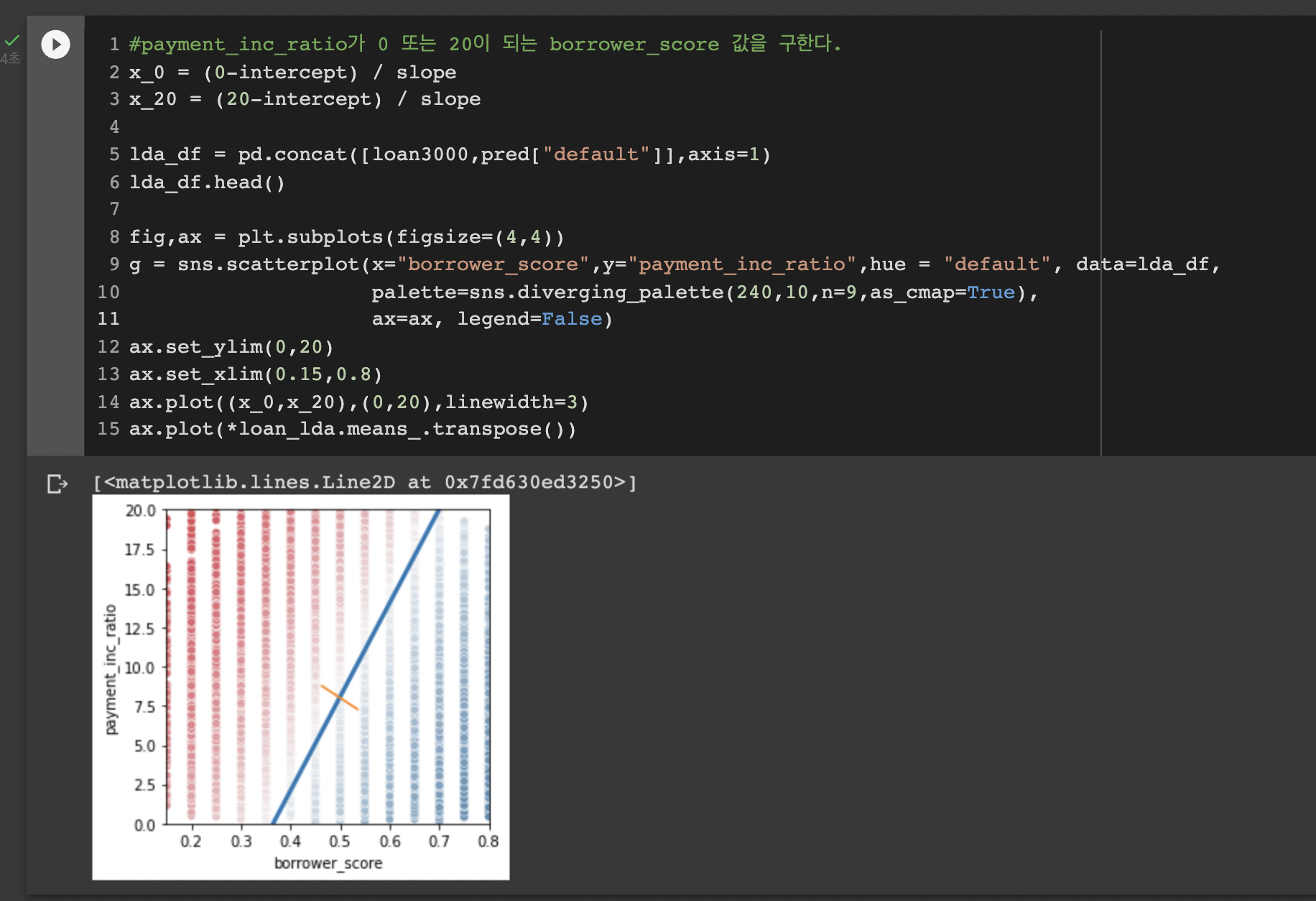
마지막으로 predict함수의 출력값을 사용하여 체납에 대한 확률값을 그래프로 시각화한다.
대각선 왼쪽의 데이터 포인트는 빨간색상으로 default(연체로) 예측됨을 알 수 있다.(확률이 0.5보다 크다는 것을 의미한다)
결국 이 대각선이 LDA에서 말하는 두 범주를 잘 구분하는 직선이고 이 선으로부터 양방향으로 멀리 떨어진 예측결과일수록 신뢰도가 높다라고 할 수 있다.




