| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 군집화
- 군집
- Clustering
- 비지도학습
- Object Detection
- GAN
- Faster R-CNN
- Fast R-CNN
- super-resolution
- hierarchical clustering
- CV
- RPN
- Deep Learning
- 이미지 초해상화
- 적대적 생성 신경망
- Region Proposal Networks
- K-means
- SRGAN
- Today
- Total
수혁지능
[Practical Statistics for Data Scientists] K-Means & Hierarchical Clustering 본문
[Practical Statistics for Data Scientists] K-Means & Hierarchical Clustering
혁수 2023. 1. 3. 01:12K-Means Clustering
Clustering(군집화)이란 데이터를 서로 다른 그룹으로 분류하는 기술을 말한다. 각 그룹에는 서로 비슷한 데이터들이 속하며, 클러스터링의 목적은 데이터로부터 유의미한 그룹들을 구하는 것이다. K-Means는 최초로 개발된 클러스터링 기법으로서 알고리즘이 상당히 간단하고 데이터가 커져도 손쉽게 사용할 수 있다는 장점이 있다.
K-Means는 데이터를 K개의 클러스터로 나눈 뒤, 할당된 클러스터의 평균(클러스터 안에 속한 레코드들의 평균 벡터)과 포함된 데이터들의 거리 제곱합이 최소가 되도록 한다. 데이터들의 거리 제곱합을 클러스터 내 제곱합 혹은 클러스터 내 SS라고도 한다. 또한, 클러스터들끼리는 최대한 멀리 떨어지도록 한다.
예시를 하나 들어보면서 K-Means에 대해 더 알아보자.
변수가 x,y 두 개이고 레코드가 n개인 데이터가 있다고 가정하자. 각 레코드 (xi,yi)를 클러스터 k에 할당하는 작업이고, 클러스터 k에 nk의 레코드가 들어 있다고 가정할 때, 클러스터의 중심은 아래 그림처럼 나타낼 수 있다.

나아가, 클러스터 내부의 제곱합은 아래 그림처럼 나타낼 수 있으며 K-Means는 모든 클러스터k의 내부 제곱합이 최소가 되도록 레코드들을 클러스터에 할당하는 방법이다.

앞서 클러스터링의 목적은 데이터로부터 유의미한 그룹을 구하는 것이라 하였는데, 일반적인 용도는 데이터에서 자연스러운 별개의 클러스터를 찾는 것이며, 응용 분야는 데이터를 미리 정해진 수의 개별 그룹으로 나누는 것이다. 여기서 각 그룹이 서로 가능한 한 다르게 나뉘었는지 확인하기 위해 클러스터링을 사용한다(가장 최적으로 그룹화하기 위해 사용).
또한, K-Means는 클러스터가 잘 분리되지 않은 경우에도 어떻게든 레코드를 클러스터에 할당한다.
K-Means 알고리즘을 글로 나타내면 다음과 같다.
1. 사용자가 미리 정해준 k값과 클러스터 평균의 초깃값을 가지고 알고리즘을 시작한다.
2. 각 레코드를 거리가 가장 가까운 평균을 갖는 클러스터에 할당한다.
3. 새로 할당된 레코드들을 가지고 새로운 클러스터 평균을 계산한다.
여기서 1번의 클러스터 평균의 초깃값은 각 레코드를 k개의 클러스터들 가운데 랜덤으로 할당한 후, 그렇게 얻은 클러스터들의 평균을 사용한다. 하지만 이것이 항상 최적의 답을 주진 않기 때문에, 랜덤하게 초깃값을 변화시키면서 알고리즘을 돌려볼 필요성이 있다. 보통 R이나 파이썬에서는 최소 10번을 반복한다. 일단 초깃값이 정해지면 반복 루프를 통해 K-Means는 클러스터 내 제곱합이 최소가 되도록 하는 해를 얻게 된다.
클러스터 해석
이러한 클러스터 분석에서 가장 중요한 부분은 바로 클러스터를 올바르게 해석하는 것이며 K-Means에서 가장 중요한 두 출력은 바로 클러스터의 크기와 클러스터 평균이다. 클러스터 평균은 앞서 정의를 했고, 클러스터의 크기는 클러스터 내부에 포함되어 있는 레코드들의 개수이다. 만약 클러스터의 크기가 유독 다른 것이 존재한다면, 이는 아주 멀리 떨어진 특이점(이상치)들이 있거나, 특정 레코드 그룹이 나머지로부터 아주 멀리 떨어져 있다는 것을 의미한다.
클러스터 개수 선정
K-Means를 사용하려면 처음에 반드시 k를 지정해야한다. k는 보통 문제가 처해진 상황에 따라 정해지는데, 예를 들어 판매 부서가 있는 회사에서는 판매 상담 전화가 필요한 고객을 특별히 따로 분류해 집중 관리하고자 할 것이다. 이럴 경우 관리를 위해 고객을 분류할 그룹 개수를 미리 결정할 수 있다. k=2이면 고객을 제대로 분류하기 힘들고, k=8이면 관리하기가 너무 많을 수 있기 때문에 그 사이의 적절한 값을 취할 것이다.
Elbow method는 이러한 k를 결정할 수 있게 해주는 하나의 통계적 접근 방식이다. 이 방법은 언제 클러스터 세트가 데이터의 분산의 '대부분'을 설명하는지를 알려준다. 여기에 새로운 클러스터를 더 추가하면 분산에 대한 기여도가 상대적으로 작아진다. 해당 시점은 누적 분산이 가파르게 상승한 다음 어느 순간 평평하게 되는 지점이며 이러한 성질 때매 Elbow라고 명명하였다. 군집 수를 점점 늘렸을 때, 군집 내 총 제곱합(SS)이 가장 크게 떨어지는 클러스터의 수를 찾는 방법과도 동일한 의미이다.
예를 들면, 아래와 같은 그림에서는 K가 2에서 3이 될때 군집 내 SS가 가장 크게 감소하므로 Elbow method에 의해 최적의 k를 3으로 정할 수 있다.

하지만 아래와 같이 k의 증가에 따라 분산 증가율이 서서히 떨어지고, 특이점이 없을 때에는 Elbow method를 적용하기 힘들다는 한계가 있다.
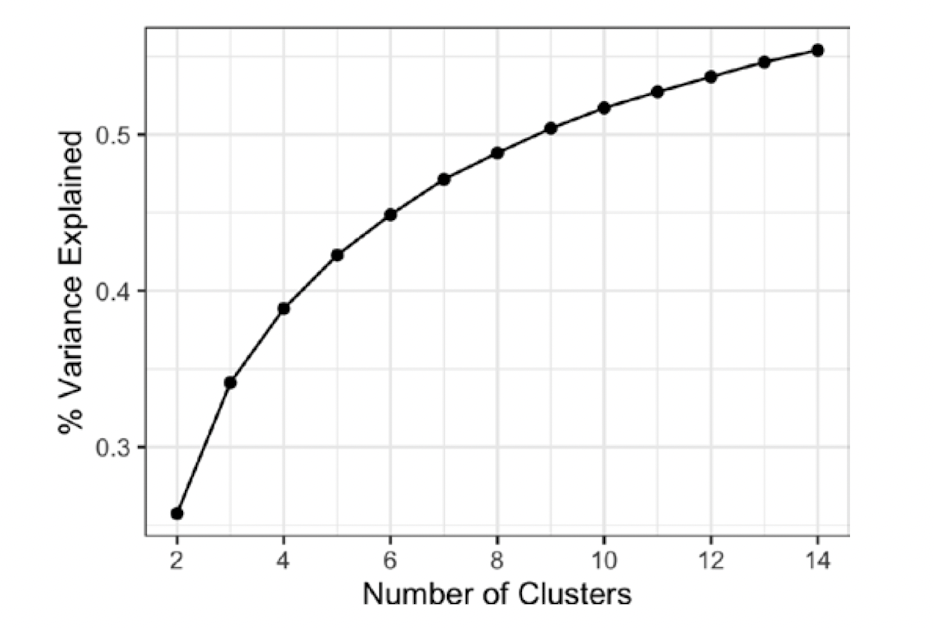
결론적으로 최적의 K를 찾는 딱 한 가지 표준화된 방법은 없다. 실제 실무에서는, 클러스터들이 새로운 데이터에서도 그대로 유지될 가능성이 얼마나 있는지, 클러스터가 해석 가능한지, 데이터의 일반적인 특성과 관련이 있는지 아니면 특정 데이터만 반영하는지 등 다양한 각도에서 평가하고 K를 정하게 된다. 일반적으로 Cross-validation을 사용하게 되면 train set이 계속 바뀌기 때문에 이러한 점들을 부분적으로 평가할 수 있다고 알려져 있다.
계층적 클러스터링(Hierarchical Clustering)
계층적 클러스터링은 K-Means 대신 사용할 수 있는 클러스터링 방법으로 K-Means와는 아주 다른 결과를 보여준다.
계층적 클러스터링은 특이점이나 비정상적 그룹,레코드를 발견하는데 더 민감하고, 직관적인 시각화가 가능하여 클러스터를 해석하기가 더 수월하다.
하지만, 계층적 클러스터링의 유연성에는 비용이 따른다. 레코드가 수만 개 이상이 되면 상대적으로 많은 컴퓨터 리소스가 필요하다. 그래서 대부분 상대적으로 데이터 크기가 작은 문제에 주로 사용되고 있다.
계층적 클러스터링은 두 가지 기본 구성요소를 기본으로 한다.
1. 두 개의 레코드 i와 j 사이의 거리를 측정하기 위한 거리 측정 지표
2. 두 개의 클러스터 a와 b 사이의 차이를 측정하기 위한, 각 클러스터 구성원 간의 거리 di,j를 기반으로 한 비유사도 측정 지표 Da,b(한 클러스터가 다른 클러스터들과 얼마나 가까운가)
여기서 가장 중요한 것은 비유사도 지표이며, 계층적 클러스터링은 각 레코드 자체를 개별 클러스터로 설정하여 시작하고 가장 가까운 클러스터를 병합하는 작업을 반복한다.
덴드로그램
계층적 클러스터링의 중요한 특징으로는 트리 모델과 같이 자연스러운 시각적 표현이 가능하다는 것이다. 이를 덴드로그램이라고 한다.
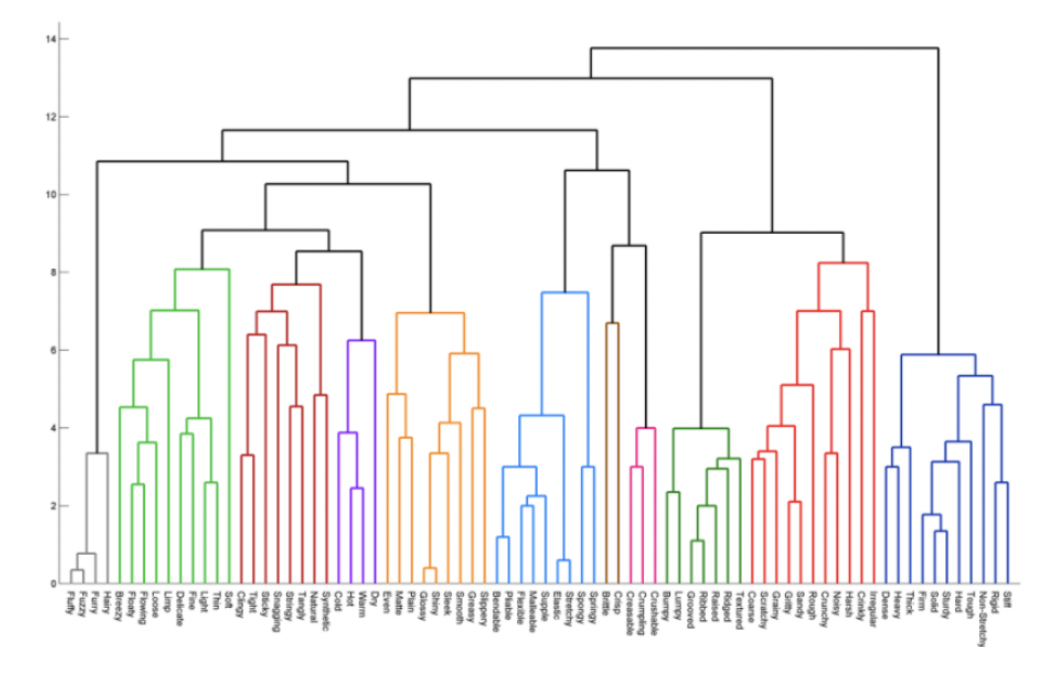
위 사진에서 트리의 잎은 각 레코드를 의미하며, 트리의 가지 길이는 해당 클러스터 간의 차이 정도를 의미한다.
K-Means와 달리 계층적 클러스터링에서는 클러스터의 수를 미리 지정할 필요가 없다. 위 사진에서와 같은 트리 구조에서 위 또는 아래로 이동하는 수평선을 이용해 서로 다른 수의 클러스터를 식별할 수 있다.
예를 들어 아래 그림에서는 덴드로그램의 최상층을 수평선으로 끊어주면 A,D,C와 B로 두 개 군집이 도출된다. 위에서 두 번째 층을 수평선으로 끊어주면 A,D와 C 그리고 B로 세 개의 군집이 도출된다.
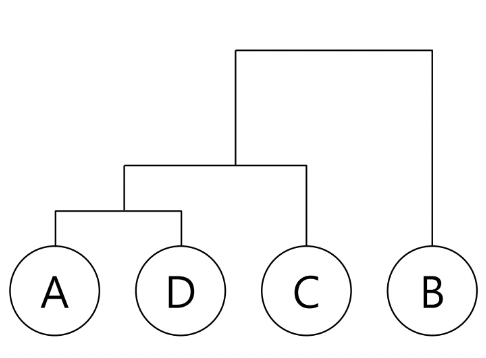
이렇게 덴드로그램을 적절한 수준에서 잘라내면 클러스터의 수를 쉽게 정할 수 있지만, 계산복잡성은 O(n3)으로 K-Means보다는 무겁다는 단점이 있다.
병합 알고리즘
계층적 클러스터링에서 가장 중요한 알고리즘은 바로 병합 알고리즘이다. 유사한 클러스터들을 반복적으로 병합하는 것으로서, 단일 레코드로 구성된 클러스터에서 시작하여 점점 더 큰 클러스트들을 만드는 것이 목표이다.
병합 알고리즘을 순차적으로 작성하면 다음과 같다.
1. 데이터의 모든 레코드에 대해, 단일 레코드로만 구성된 클러스터들로 초기 클러스터 집합을 만든다.
2. 모든 쌍의 클러스터 k,l 사이의 비유사도 D(Ck,Cl)을 계산한다.
3. D(Ck,Cl)에 따라 가장 가까운 두 클러스터 Ck와 Cl을 병합한다.
4. 둘 이상의 클러스터가 남아 있으면 2단계로 다시 돌아간다. 그렇지 않고 클러스터가 하나라면 알고리즘을 멈춘다.
2번에서의 비유사도 지표를 계산하는 것이 중요한데, 계산 방식에는 일반적으로 4가지가 존재한다.
1. 완전연결(Complete linkage)
클러스터 A와 B 사이의 모든 레코드 쌍의 최대 거리를 사용하는 방식이다.
비슷한 멤버가 있는 클러스터를 만드는 경향이 있다.
2. 단일연결(Single linkage)
클러스터 A와 B 사이의 모든 레코드 쌍의 최소 거리를 사용하는 방식이다.
Greedy한 방법이며, 서로 크게 다른 요소들도 하나의 클러스터에 포함되는 일이 생길 수 있다.
3. 평균연결(Average linkage)
클러스터 A와 B 사이의 모든 레코드 쌍의 거리의 평균을 사용하는 방식이다.
1과 2를 절충한 방식이다.
4. 최소분산(Minimum variance) = Ward's method
클러스터 내 제곱합(SS)를 최소화하는 방식으로 K-Means와 유사하다.
4가지 방식 모두 레코드 쌍의 거리를 계산할 때는 일반적으로 유클리드 거리를 사용한다.
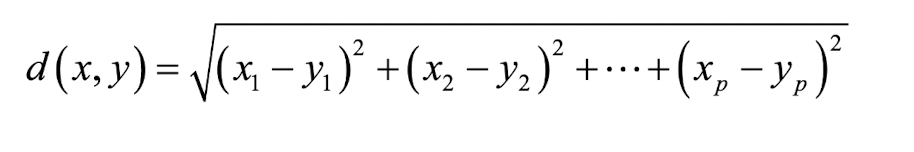
아래 그래프는 이러한 4가지 방식으로 계층적 클러스터링을 수행한 결과이다.
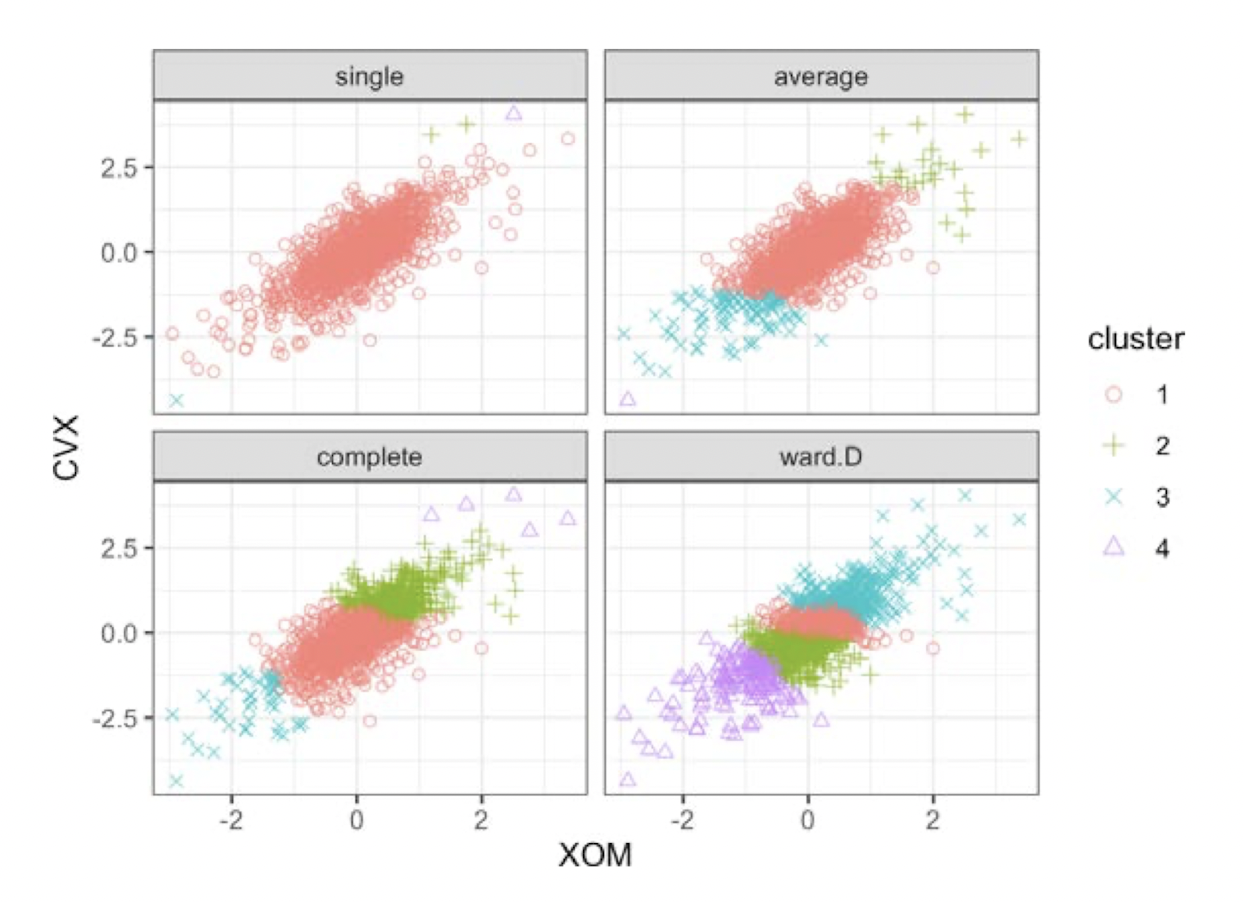
Single(단일 연결) 방식은 거의 모든 점을 하나의 클러스터에 할당했다. Ward(최소 분산)을 제외한 다른 방법은 외곽에 요소가 몇 개 없는 특이점들로 이루어진 작은 클러스터를 만들었다. Ward는 K-Means와 가장 유사한 결과를 보인다.




