| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- Object Detection
- Fast R-CNN
- 적대적 생성 신경망
- RPN
- 비지도학습
- super-resolution
- Deep Learning
- hierarchical clustering
- Faster R-CNN
- SRGAN
- Clustering
- CV
- 군집
- K-means
- 군집화
- 이미지 초해상화
- Region Proposal Networks
- GAN
- Today
- Total
수혁지능
[Practical Statistics for Data Scientists] Random Sampling and Sample Bias 본문
[Practical Statistics for Data Scientists] Random Sampling and Sample Bias
혁수 2022. 3. 17. 01:53빅데이터 시대가 되면서 표본추출은 필요 없다? No!
데이터의 크기는 많이 늘어났지만 데이터의 질과 적합성을 담보할 수 없는 실태 >> 표본추출은 여전히 필요하다
빅데이터 프로젝트도 작은 표본 데이터를 가지고 예측 모델 개발 후 테스트함.

모집단에서 표본 데이터를 추출하는 것 : 표본추출
데이터 과학자들은 표본추출 과정과 주어진 데이터에 집중해야 함.
모집단에 대한 이해를 바탕으로 추가적인 통찰을 얻을 수 있는 경우: 모델링이 가능할 때 ex) coin flip(이항 분포)
RandomSampling : 무작위로 표본을 추출하는 것(모든 원소는 동일한 확률로 selected) / 추출된 샘플 = simple random sample
-복원 추출: 추첨 후 , 다음번에도 중복 추출 가능
-비 복원 추출: 한번 뽑힌 원소는 추후 추첨에 사용하지 않음
샘플 기반의 추정이나 모델링에서 데이터 품질(완결성, 형식의 일관성, 깨끗함 및 데이터의 정확성+ 대표성)은 데이터 양보다 더욱 중요.
그런데 원래 대표되도록 의도된 모집단으로부터 추출되지 않고 유의미한 비임의 방식으로 표본이 추출될 수도 있다(표본 편향)
ex) 특정 경험이 있었던 특정 가게에만 SNS 리뷰를 남기는 자기 선택 표본 편향
즉, 아무리 random sample이어도 어떤 표본도 모집단을 정확하게 대표할 수 없다.
Bias
측정 과정 혹은 표본추출 과정에서 발생하는 systematic 오차.
random sampling으로 인한 오류: 오류가 존재하지만 오류의 분포는 랜덤 하다.(치우치는 경향 x)
bias으로 인한 오류: 오류가 존재하지만 오류의 분포가 한쪽으로 치우친다.

Random Sampling(임의 표본추출)
대표성을 담보하는 핵심 개념 >> bias를 줄이고 품질 향상을 용이하게 한다.
EX) 파일럿 고객 설문 조사 준비 for 고객의 대표 프로필 만들기
1. 접근 가능한 모집단을 적절하게 정의 ( 고객이 누구인가? >> 모든 과거 고객 포함? , 환불 고객 포함? , 내부 구매자 포함?.. etc)
2. 표본추출 절차를 정의 (무작위로 100명 선택 or 시기를 잘 나눠서 무작위 추출(평일 오전, 평일 오후, 주말 오전, 주말 오후))
+ stratified sampling 활용: 모집단 여러 층으로 나누고, 각 층에서 무작위로 샘플 추출.
>> 일반 random sampling에서 특정 층이 적게 나올 때, 해당 층에 높은 가중치 부여해 sample 크기 맞추기
Q1 : 그렇다면 이렇게 sampling을 잘해서 bias를 줄이고 데이터 품질을 높이면 되는데 빅데이터는 왜 필요한가?
A: 데이터가 크고 동시에 희소할 때는 volume이 적으면 부정확한 결과 반환. ex) 구글의 검색 쿼리
방대한 양의 데이터가 누적될 때만 대부분의 쿼리에 대해 효과적인 검색 결과 반환
실제 연관된 레코드(정확한 검색 쿼리 or 아주 비슷한 쿼리가 들어 있는 레코드)의 수는 수천 개 정도만 돼도 유의미.
But 수천 개의 레코드를 위해서는 수조 개의 데이터 필요
Q2: 표본 평균과 모평균을 굳이 구분하는 이유는?
A: 표본에 대한 정보는 관찰을 통해 얻어지지만, 모집단에 대한 정보는 작은 표본들로부터의 추론으로 얻어진다.
Selection Bias(선택 편향)
관측 데이터를 선택하는 방식 때문에 생기는 편향
탐구의 2가지 방식
1. 연역적 방식(가설 세우고 잘 설계된 실험 수행) >> 결과에 대한 확신 가능
2. 귀납적 방식(가지고 있는 데이터 확인 후 그 안에서 패턴 찾기) >> 패턴에 대한 의심이 필요( 믿을 만한 패턴인가?)
선택 편향의 종류(귀납적 방식에서 발생)
1. 흥미로운 결과가 나올 때까지 데이터 마이닝에서의 모델 반복 실행 (Vast Search Effect)
-흥미로운 결과는 의미가 있는 것인가? 우연히 얻은 예외인가?
-ex) 동전 10번 던져서 모두 앞면이 나오는 경우
2. 연구 시의 Data Snooping(흥미로운 것을 찾기 위해 데이터 너무 많이 살펴 봄)
-test set을 바탕으로 모델을 정하게 되면 일반화 오차 측정 시 너무 낙관적으로 추정됨, 실제는 성능 안 나옴
3. Nonrandom sampling
4. 데이터 체리 피킹(선별) : 특정 조건에 맞는 데이터만 사용
5. 특정한 통계적 효과를 강조하는 시간 구간 선택
6. 흥미로운 결과가 나올 때 실험 중단 : 일부분의 데이터만 사용
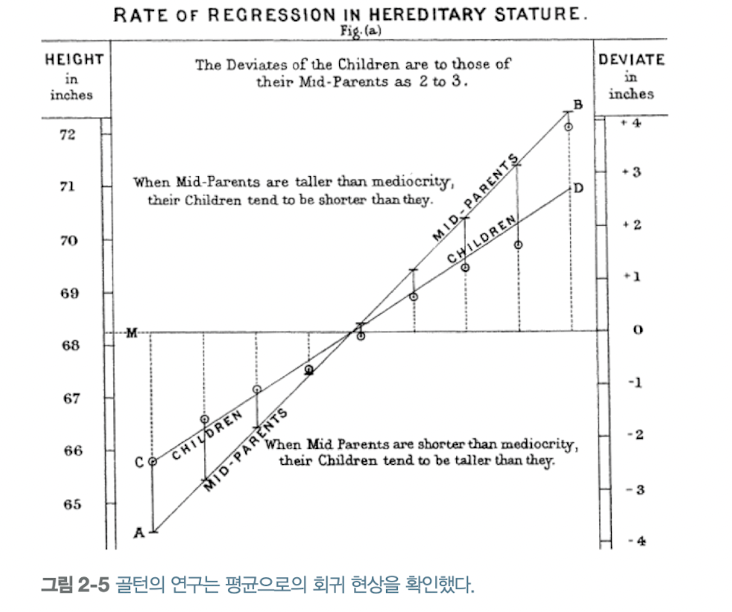
7. 예외 결과에 너무 의미를 부여할 때(평균으로의 회귀 무시) : 극단적 결과
cf) 평균으로의 회귀: 주어진 어떤 변수를 연속적으로 측정했을 때, 예외적인 경우가 관찰되면 그다음에는 중간 정도의 경우가 관찰
선택 편향을 방지하는 법
1. 가설을 구체적으로 명시하고, 정확한 randomsampling 수행(적절한 모집단 정의, 표본추출 방법 선택)
2. 성능 검증할 때는 둘 이상의 holdout set 사용
-주어진 데이터를 랜덤 하게 두 개 이상의 분류로 분리하여 검정을 실시 (ex) train data / test data + validation data)
3. target shuffling(순열 검정) 이용해 데이터 마이닝 모델 예측 검정
-비모수 통계 기법이기 때문에 정규분포 가정이 없어도 검정 가능
-순열 검정의 핵심 idea: 두 표본 그룹이 동일한 모집단에서 추출되었다고 한다면, 두 그룹 안에 있는 샘플들을 교환한 뒤 통계적으
로 검증해도 여전히 두 그룹 간에는 차이가 없어야 한다.
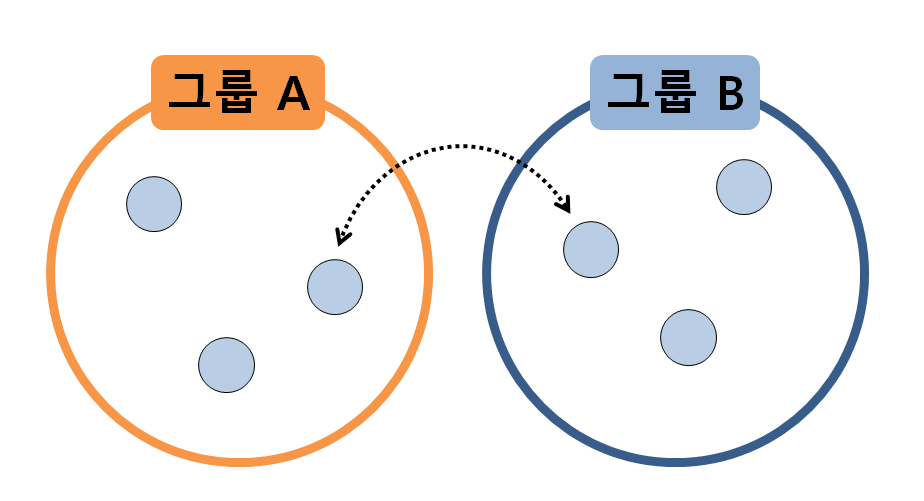
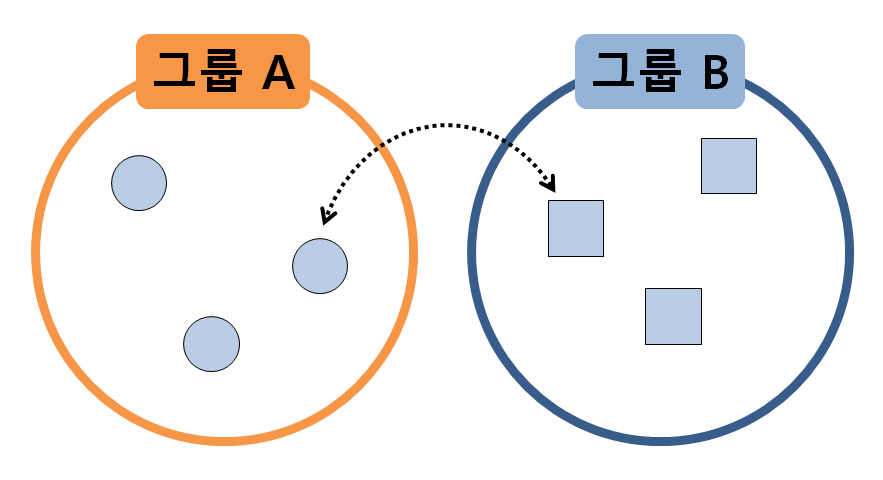
-샘플들을 섞어가면서 통계량 여러 번 추출 >> 추출된 통계량 분포 확인
예시. 두 그룹의 샘플 데이터, 관찰하고자 하는 통계량: 평균의 차이
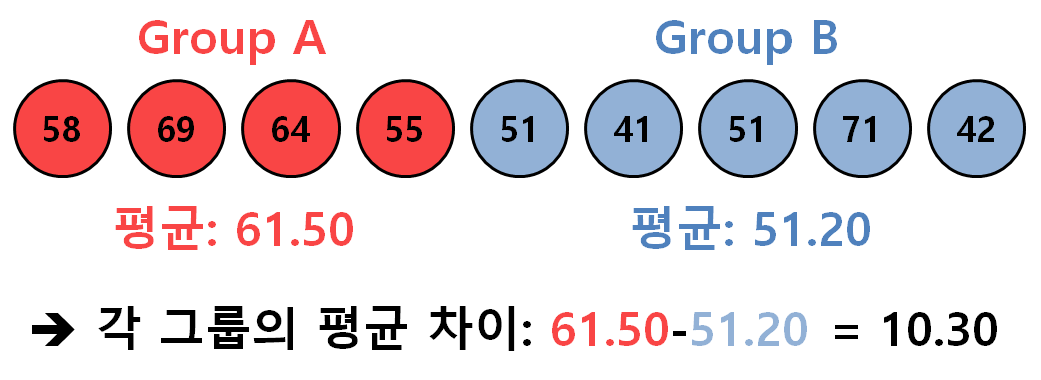
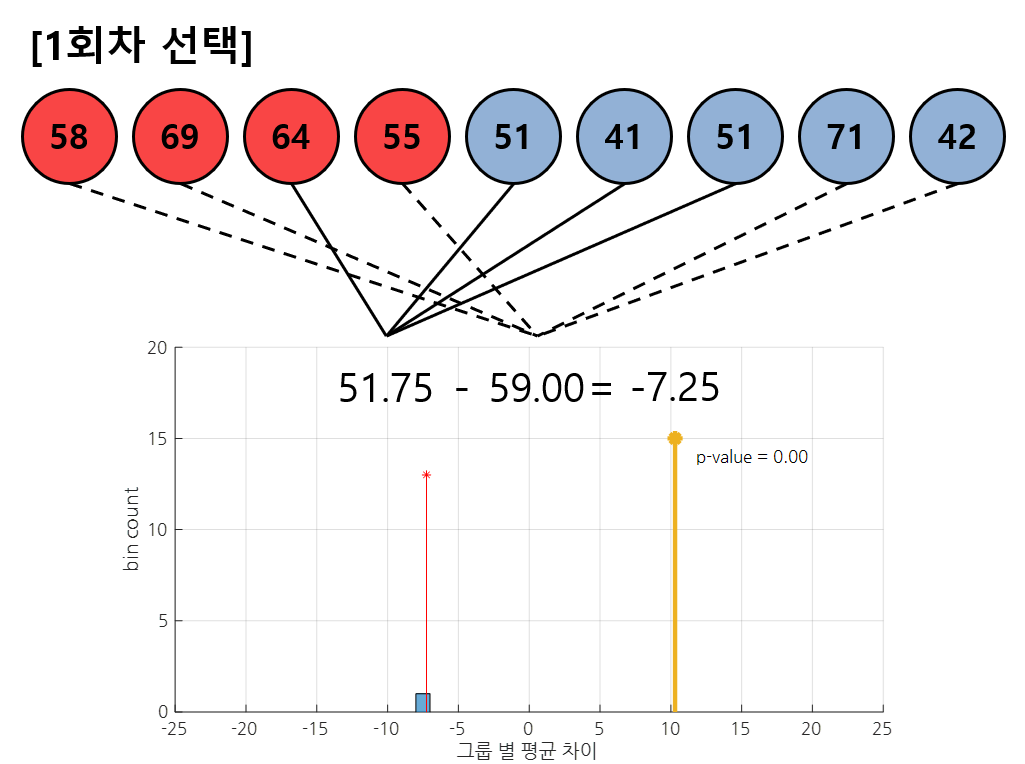
n회차 shuffling 진행 후 나온 통계량(그룹의 평균 차이)의 분포를 확인, 처음에 주어진 통계량 값(10.3)의 위치 확인(by pvalue)
(여기서 pvalue = (10.3 보다 큰 통계량의 개수 / 전체 shuffling 횟수)로 계산 가능)
결론
p-value 값이 유의수준보다 작다면, 귀무가설 기각(=동일한 모집단에서 추출되지 않음) +
통계적으로 유의미(statistically significant)
p-value 값이 유의수준보다 크다면, 귀무가설 기각 불가. 어떤 것도 증명할 수 없다.
출처: https://angeloyeo.github.io/2021/10/28/permutation_test.html
더 읽어볼 자료
- Sampling Methods for Online Surveys, Ronald Fricker / 표본추출 절차에 대한 리뷰 https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.720.4424&rep=rep1&type=pdf
- Fooled by Randomness Through Selection Bias / 주식시장 매매 방식의 선택편향 리뷰 https://www.priceactionlab.com/Blog/2012/06/fooled-by-randomness-through-selection-bias/
Fooled by Randomness, Over-fitting And Selection Bias – Price Action Lab Blog
There are software programs that allow combining technical indicators with exit conditions for the purpose of designing trading strategies that fulfill desired performance criteria and risk/reward objectives. Due to data-mining bias it is very difficult
www.priceactionlab.com




