| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- CV
- Deep Learning
- K-means
- Object Detection
- 적대적 생성 신경망
- 이미지 초해상화
- RPN
- hierarchical clustering
- 군집화
- Fast R-CNN
- 군집
- GAN
- Clustering
- Region Proposal Networks
- 비지도학습
- super-resolution
- SRGAN
- Faster R-CNN
- Today
- Total
수혁지능
[Practical Statistics for Data Scientists] Multi-Armed Bandit Algorithm 본문
[Practical Statistics for Data Scientists] Multi-Armed Bandit Algorithm
혁수 2022. 3. 31. 02:37 이 글은 데이터 과학을 위한 통계(앤드루 브루스) 및 다양한 블로그를 참고했음을 미리 밝힙니다.
참고문헌은 맨 밑에 기재해놓았습니다.
전통적인 A/B 검정의 한계
A/B 검정은 두가지 처리방법, 제품, 절차 중 어느 쪽이 다른 쪽보다 더 우월하다는 것을 입증하기 위해 실험군
두 그룹으로 나누어 진행하는 실험. 둘 중 더 좋은 방법을 얻게 되면 실험을 멈추고 결과에 따라 행동하게 됨. 웹 디자인이나 마케팅에서 일반적으로 사용되는 방법!
하지만 이러한 접근에 몇가지 어려움이 존재
- 결론을 내리기 어렵다
-실험 결과가 한쪽으로 나와도(더 좋은 효과), 충분한 크기의 표본이 없다면 입증불가능 - 실험이 끝나기 전, 이미 얻은 결과들을 이용 시작 가능
-테스트를 다 했을 때 B가 더 좋다고 나왔는데, 지금까지는 A를 사용하고 있어서 손해를 보았다 - 실험이 끝난 후에도 추가적인 데이터에 대한 실험가능성 존재
-테스트를 할때는 A가 좋았는데, 시간이 좀 지나니 B의 반응률이 더 좋아졌다 - 테스트를 하는 데 오래걸리고 비용도 많이 드는 편이다
실험과 가설검정을 바탕으로 한 전통적인 방법이기 때문에 유연하지 않다. 특정 처리 방법의 효과에 대한 정적인 질문에 답하는 데 초점.이분법적인 한계도 존재(A가 낫냐 아니면 B가 낫냐, 다른 대안X)
멀티암드 밴딧 알고리즘(MAB)의 등장
데이터 과학자들과 산업계에서는 "가격 A와 가격B의 차이가 통계적으로 유의한가?"라는 질문보다는 "가능한 여러 가격 중에서 가장 좋은 가격은 얼마일까?"라는 질문에 더 관심이 있다. 즉, 두 가지 상태를 비교하는 것보단 한번에 여러 가지 상태를 신속하게 비교하는 것을 원한다. 또한, 통계적 유의성보다는 비용과 결과를 최적화하는 것을 원한다.
컴퓨터와 소프트웨어의 발전에 힘입어 이러한 니즈를 충족시키고 A/B test의 한계를 보완하기 위해 멀티암드 밴딧 알고리즘이 등장하였다.
멀티암드 밴딧 알고리즘은 재미있게도 카지노의 슬롯머신에서 나오게 되었다. 슬롯머신은 손잡이를 당겼을 때 화면의 무늬가 돌아가게 되는데, 당첨이되면 돈을 따고 그렇지 않으면 돈을 잃는 도박기기이다. 여기서 이제 둘 이상의 손잡이나 둘 이상의 슬롯머신이 있을 때, 최적의 수익을 내려면 어떤 손잡이를 당길 것인지, 어떻게 슬롯머신들에 투자를 할지 만들어진 알고리즘이 바로 멀티암드 밴딧 알고리즘이다.

멀티암드 밴딧 알고리즘(MAB)의 방식:
탐색(Exploration)과 활용(Exploitation)의 조화
우리가 카지노에 있다고 상상해보면서 본격적으로 멀티암드 밴딧 알고리즘에 대해 알아보자.
우리 앞엔 둘 이상의 손잡이가 달려 있고 각 손잡이는 각각 다른 확률로 보상을 주는 슬롯머신이 있다.
우리의 목표는 가능한 한 많은 돈을 얻는 것이고, 많은 보상이 나오는 손잡이를 최대한 빨리 확인하는 것이다.
우리는 제한된 돈을 가지고 있기 때문에 두가지 선택을 할 수 있는데,
첫째는 "어떤 손잡이가 얼마의 보상을 주는지 탐색하는 것"(Exploration)이고
둘째는 "탐색 정보를 활용하여 돈을 뽑아먹기"(Exploitation)이다.
첫째방식만을 취하면 모든 손잡이의 보상확률을 구해야하므로 최대한 랜덤하게 손잡이를 당길 것이고 그렇게 되면 보상이 낮은 손잡이도 필연적으로 당기게 된다.
둘째방식만을 취하면 초기 탐색 정보를 바탕으로 가장 보상이 잘나온 손잡이만을 당기게 되는데 탐색이 충분치 않아 사실은 나머지 손잡이가 더 좋을 수도 있다.(Greedy Algorithm)
이렇게 하나의 선택만을 가지고서는 최대한의 돈을 벌기 어렵다. 따라서, 밴딧 알고리즘은 하이브리드 방식을 사용한다.
Greedy Algorithm
하이브리드 방식을 소개하기 전에 잠깐 언급했던 Greedy Algorithm에 대해 좀 더 살펴보자.
간단히 말하자면, 초기 탐색 중 가장 평균 보상이 높았던 손잡이를 하나 선택하고, 그것에 몰빵하는 전략이다.
이를 수식적으로 표현해보자.
q*(a)는 a손잡이를 당기는 행동의 실제가치, a는 손잡이에 대한 변수이고, t는 시점, A는 action, R은 reward를 의미한다.

현실에서는 이 값을 모르기 때문에 아래와 같은 추정 값을 사용한다(Sample-Average Method) (Qt(a) = 추정 가치)

이를 이용해 Greedy Algorithm에서 우리가 선택할 Action은 Qt(a)를 최대로 만들어주는 손잡이 a를 당기는 것이다.
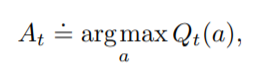
Epsilon-Greedy Algorithm
Greedy Algorithm은 매우 간단하고 매력적인 알고리즘이지만, 선택된 손잡이가 실제로 가장 좋은 손잡이가 아닐 수도 있다.
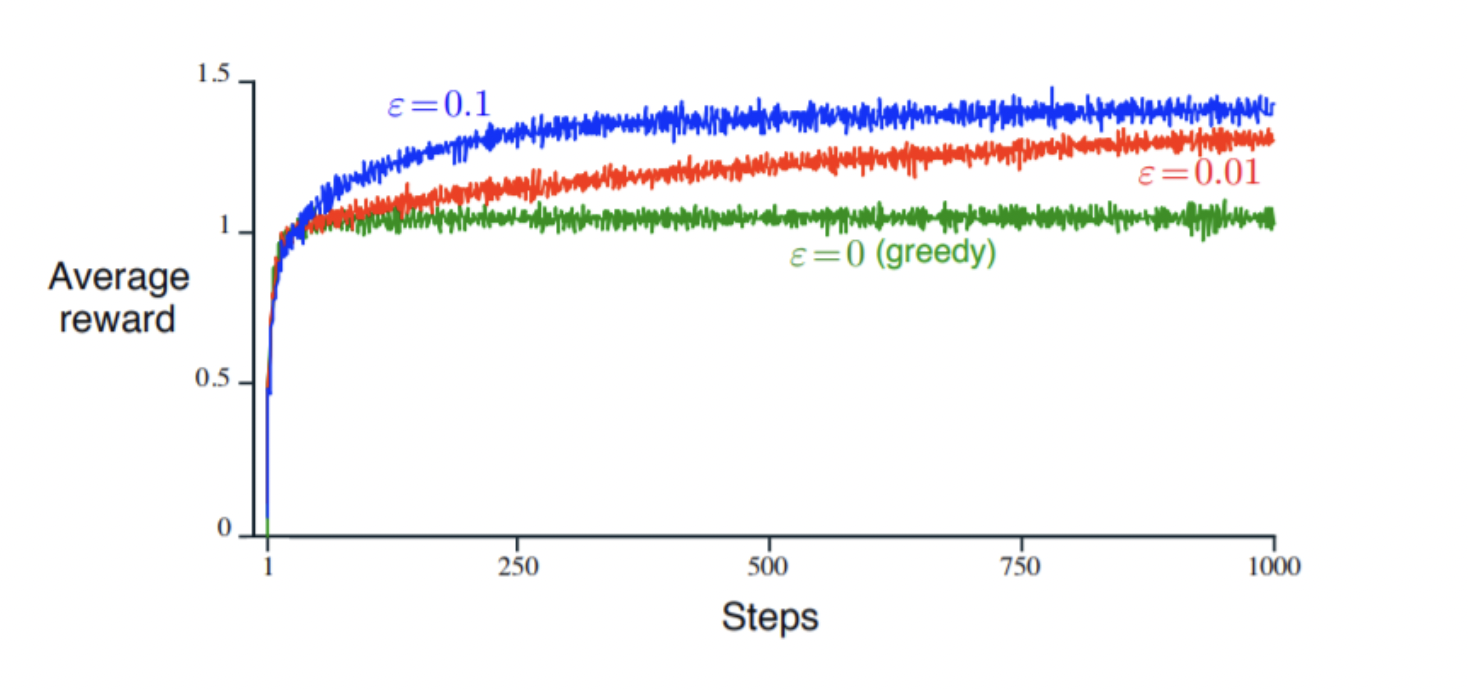
여기에 "탐색"을 추가한 알고리즘이 바로 Epsilon-Greedy Algorithm이다. ε이라는 0과 1 사이의 아주 작은 값을 잡아서(유일 파라미터), ε의 확률로 "탐색"을 적용하고 1-ε의 확률로 "활용"을 적용해 Greedy Algorithm을 사용하게 된다. 이렇게 되면 대부분의 경우는 현재 상태의 최선의 행동을 하되, 가끔은 무작위로 행동하게 된다.
그러나 입실론이 지나치게 작으면 "탐색"이 잘 이루어지지 않아 Greedy해지고, 지나치게 크면 최선의 행동을 아는 상황에서도 불필요하게 탐색이 많아지는 경우가 생긴다. 또한, 여전히 탐색의 방법이 무작위적이라는 한계가 있다. 만약 10개의 행동이 있고 이 중에 2개 중 하나가 최선인 상황이라고 해도 Epsilon-Greedy Algorithm은 나머지 8개도 모두 공평하게 탐색한다.

가치 추정의 다른 방법
여기서 잠깐 Qt(a), 즉 추정 가치를 계산하는 다른 방법에 대해서 알아보자. 맨 처음 Greedy Algorithm에서 추정 가치를 계산한 방식은 그냥 보상(R)의 평균을 구하는 것이었다.
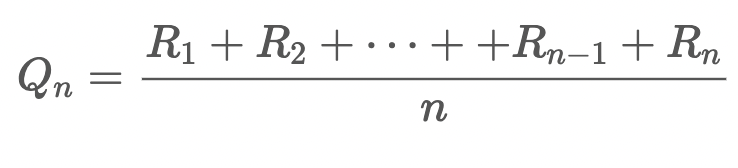
여기서 이 식을 아래와 같이 점화식 형태로 변경할 수 있다.
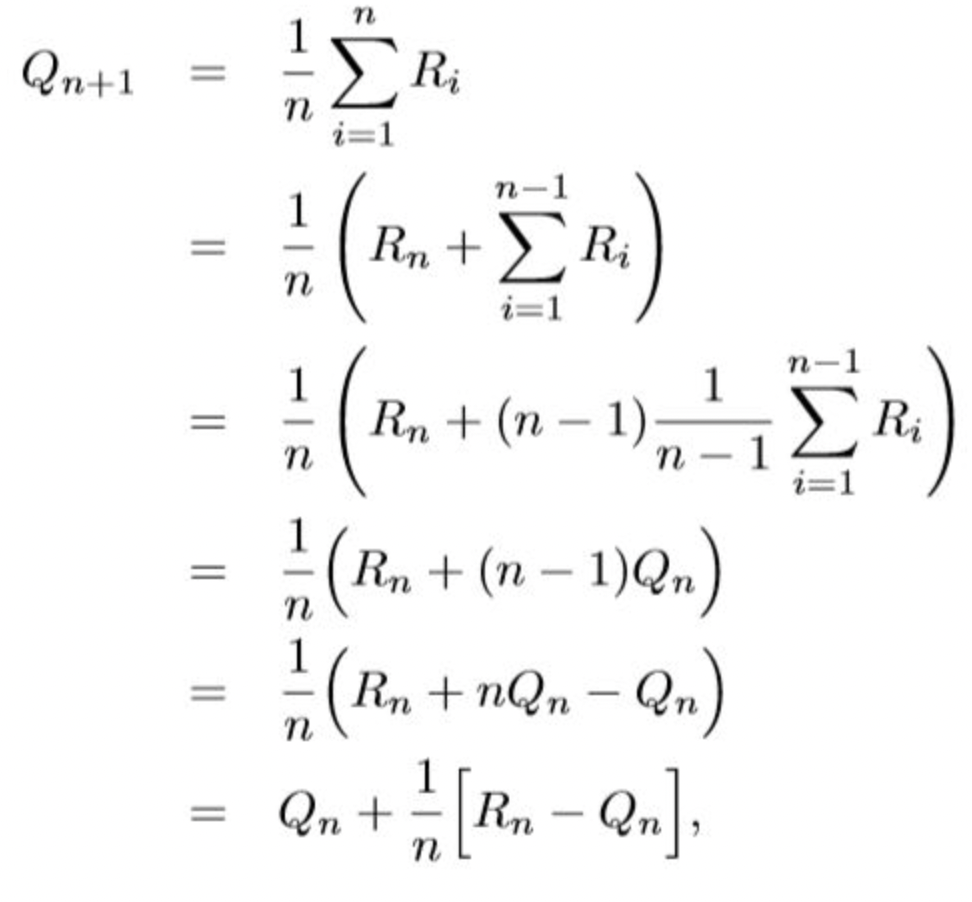
이렇게 되면 보상의 총합을 모르더라도, 바로 직전의 추정가치 Qn과 직전의 보상 Rn만 있으면 현재 시점의 가치(Qn+1)를 추정할 수 있다.
위의 가치 추정법은 stationary(보상확률이 시간에 따라 변하지 않음)한 problem에 대해 적용할 수 있다.
그런데 만약 슬롯머신의 보상확률이 유동적으로 계속 변화한다면(nonstationary), 최근에 받은 reward에 오래전에 받은 reward보다 가중치를 더 많이 줘야 할 것이다. 이 때 사용하게 되는 방식이 지수이동평균(exponential moving average)이다.
stationary식에서 1/n을 α로 바꿔서 식을 수정하면 아래와 같은 형태가 나오게 된다
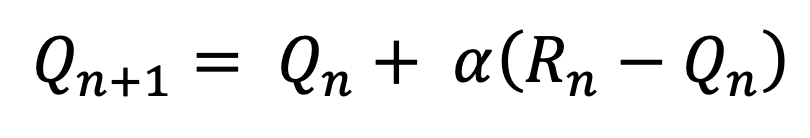
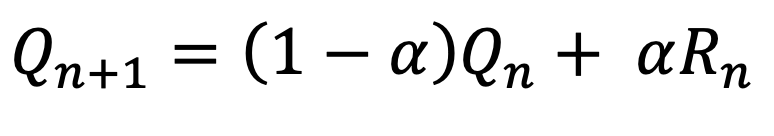
직전의 추정가치는 (1-α)비율로, 직전의 보상은 α의 비율로 가치에 추가된다.
위 식을 이용해 추정 가치 Q를 풀어나가면 최종적으로 아래와 같은 형태가 된다.
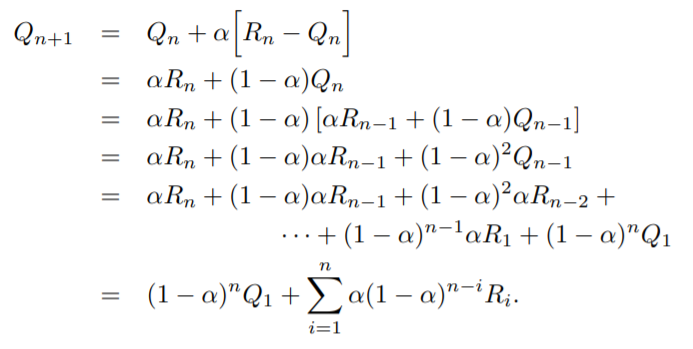
여기서 우리는 과거의 보상(R)이 n-i에 따라 weighted 되어져, 현재 시점의 추정가치(Qn+1)에서 차지하는 비중이 시간이 흐를수록 낮아진다는 것을 알 수 있다.(0<α<1) (Qn+1에서의 비중: R1 < R2 < R3 ... <Rn)
이를 통해 MAB를 적용해야 할 상황이 stationary인지, nonstationary한지에 따라 가치를 추정하는 방식을 다르게 설정해야 한다는 것을 알 수 있다.
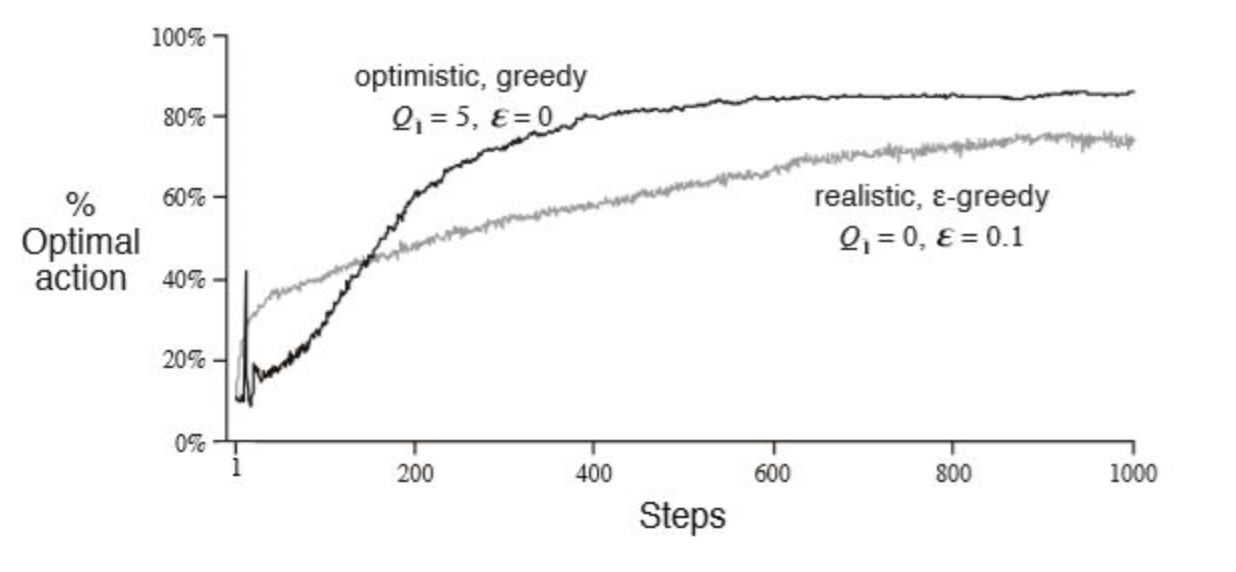
Optimistic Greedy Algorithm
stationary(sample average), nonstationary(weighted average) 상관없이 슬롯머신을 당기기 전에는 추정가치를 계산할 수 없다. 그렇기 때문에 Q1은 일반적으로 0으로 초기화를 한다(realistic method). 그런데 Optimistic 방법에서는 초기 추측값을 reward보다 더 크게 줘서 오히려 손잡이를 당기면 추정 가치가 떨어지게 한다. 그러면 "탐색"을 촉진시켜 초기에 선택이 안된 손잡이를 선택하게 된다.
nonstationary상황에서는 갈수록 초기값의 영향력이 줄어드므로, 시간이 지나면 "탐색"이 줄어들고 greedy한 손잡이를 "활용"하게 된다. 그렇기 때문에 지수이동평균과 함께 사용되면 입실론이 없어도 Epsilon-Greedy Algorithm 이상의 성능을 낼 수 있다.
UCB Algorithm
Epsilon-Greedy Algorithm의 무작위적 탐색을 해결하기 위해 나온 알고리즘이 UCB(Upper-Confidence-Bound) Algorithm이다.
이것의 핵심 아이디어는 추정가치에서 일종의 신뢰구간(오차범위)을 구해서 그 구간의 위쪽이 높은 행동을 선택하는 것이다.
UCB 알고리즘을 수식화하면 다음과 같다.
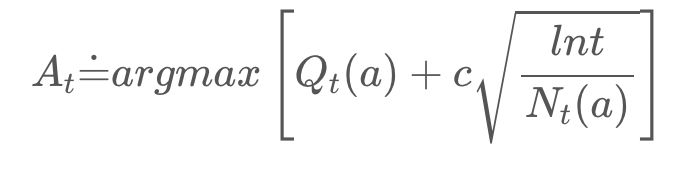
추정가치 Qt(a)에다 upper bound를 더한 모습인데 이 upper bound는 Qt(a)의 불확실성이라 생각하면 된다.
오른쪽항의 는 하이퍼파라미터로, "탐색"의 정도를 결정하는 값이다. 를 크게 하면 (신뢰구간이 넓음) "탐색"을 많이 하게 되고 작게 하면(신뢰구간이 좁음) "활용"을 많이하게 된다(Epsilon-Greedy Algorithm의 ε와 비슷함). lnt는 시점 t에 을 취한 값이고, 는 손잡이 a를 당긴 횟수이다. 분산 대신 lnt이 들어간 점이 기존의 신뢰구간과 다른점이라고 할 수 있다.
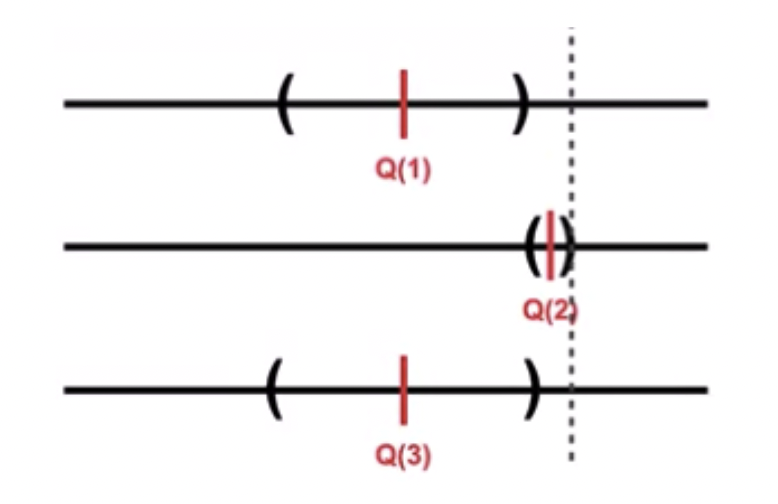
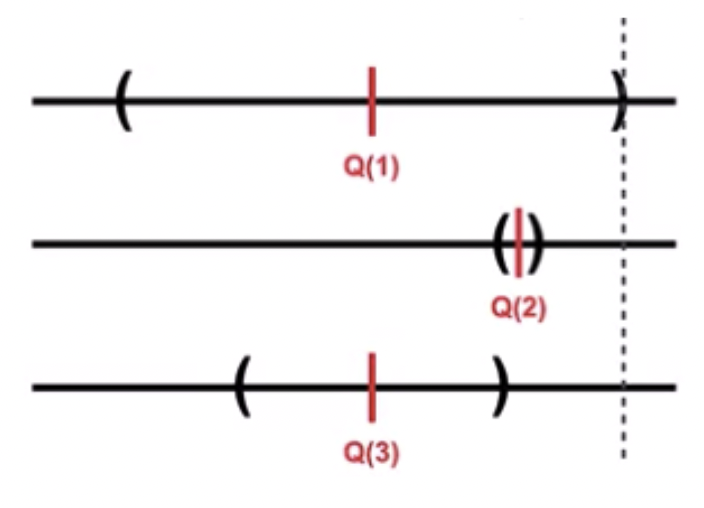
앞의 그림은 추정가치가 가장 높은 2번이 upper bound도 가장 높아 선택되었다. 신뢰구간의 크기도 작아 불확실성도 적으니 높은 보상을 얻을 수 있을 것이다("활용") 뒤의 그림은 추정가치는 낮지만 boundary의 크기가 큰(불확실성이 높은) 1번이 선택되었다("탐색")
즉, UCB는 추정 가치 와 이제까지 행동을 한 횟수 두 가지를 모두 고려하여 탐색을 하므로 좀 더 효율적인 탐색을 할 수 있게 해준다. 무작위로 탐색을 하는 것이 아닌, boundary 안에서 optimal이 될 수 있는 잠재력 높은 손잡이만 선택한다.
UCB 알고리즘은 MAB에서 가장 각광받고 있는 알고리즘 중 하나이며 성능도 앞의 두 가지 알고리즘보다 더 우수하다.
Thompson Sampling
UCB Algorhithm과 함께 밴딧 문제를 해결하는 방법 중 가장 많이 활용되는 알고리즘이 있다. 바로 Thompson Sampling이다. Google Analytics에서도 사용하고 있는 알고리즘으로 이론적,실험적인 측면에서 모두 두각을 나타낸다.
Thompson Sampling은 베이즈 방식을 사용한 알고리즘으로서 베타 분포를 사용하여 수익(목표)의 일부 사전분포를 가정한다(문제 상황이 베르누이 분포를 따를 때). 가정 안에서 각 추출 정보가 누적되면서 정보가 업데이트 되고, 그 덕분에 다음번에 최고 손잡이를 선택할 확률을 효과적으로 최적화 할 수 있다. (베이즈 방식: 모수를 확률변수로 생각하여 그에 대한 사전정보 활용하여 모수 추정)
Thompson Sampling은 위에서 소개한 알고리즘들보다 더 복잡하므로 예시를 들어 설명하려 한다. 밴딧 알고리즘은 웹 테스트에서 널리 사용되기 때문에 일상생활에서 자주 시청하는 유튜브 썸네일 별 영상 클릭 확률을 알아보도록 하자.
본격적인 예시 설명에 앞서 Thompson Sampling의 핵심인 베타 분포에 대해 간단히 알아보자. 베타 분포는 두 매개변수 와 에 따라 [0, 1] 구간에서 정의 되는 연속확률분포이고, 확률을 random variable로 정의한 확률에 대한 확률분포이다. 두 매개변수는 양수여야 하며 보통 사전정보가 없을 때 베타 분포를 많이 가정한다. 매개변수에 따라 다양한 형태로 변형이 가능하기 때문이다.
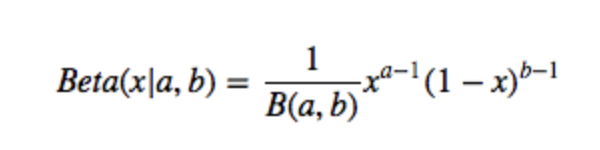
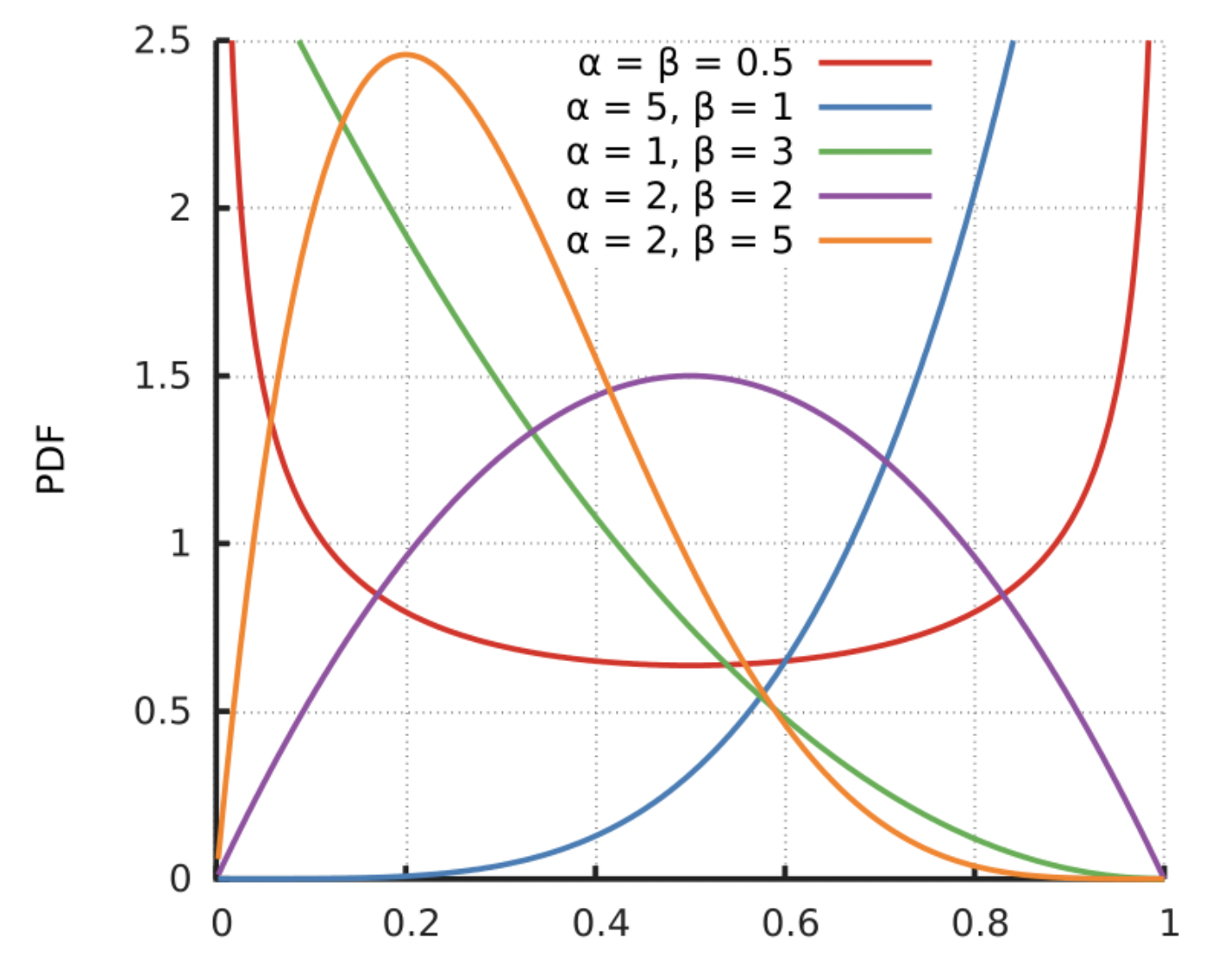
현재 우리에게 유저에게 노출시키고 싶은 유튜브 썸네일 1,2,3이 있다고 가정하자. 각각의 썸네일들을 유저들에게 보여줬을 때 영상을 클릭할 확률을 알고 싶다. 우리의 목표는 가장 많은 클릭수를 불러오는 최적의 썸네일을 찾는 것이다. (아래의 실험은 사고실험으로 진행되었다)
여기서 썸네일을 클릭하는 것은 베르누이 분포를 따른다.(클릭할 확률은 θ이고, 경우의 수는 클릭하거나 클릭하지 않는 것 2개)
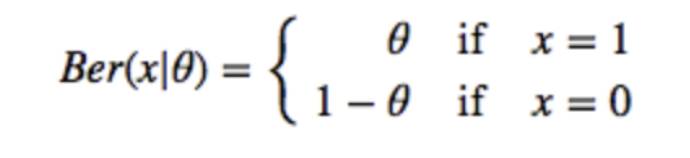
앞에서도 언급했듯이 Thompson Sampling의 핵심은 베타 분포이고 베타 분포의 매개변수는 와
썸네일을 보고 클릭한 횟수 = 0, 썸네일을 보고 클릭하지 않은 횟수 = 0 (Beta(1,1))
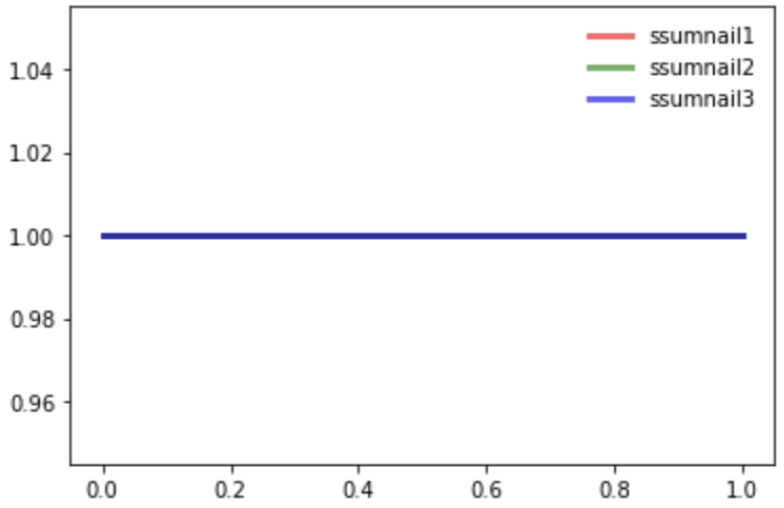
2. 썸네일 1: 노출 후 클릭, 썸네일 2: 노출 후 클릭X, 썸네일 3: 노출 X
원래는 샘플링을 하여 썸네일을 선택해야 하지만, 데이터가 너무 없으므로
썸네일을 랜덤하게 노출시켜보고 반응을 살펴보도록 하자.
ssumnail1 : Beta(2,1)
ssumnail2 : Beta(1,2)
ssumnail3 : Beta(1,1) (노출시키지 않았으므로, 클릭의 여부 세지 않는다)
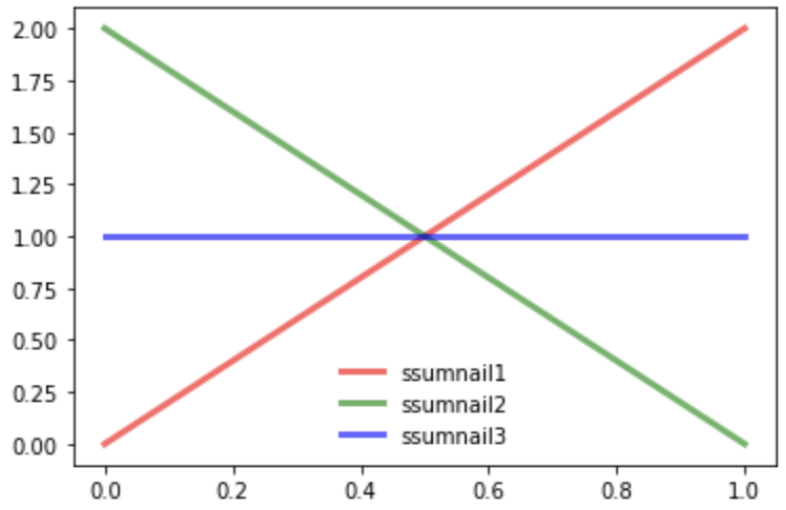
3. 썸네일 1: 노출 후 클릭/노출 후 클릭X, 썸네일 2: 노출 후 클릭/노출 후 클릭X, 썸네일 3: 노출 후 클릭X/노출 후 클릭
ssumnail1 : Beta(3,2)
ssumnail2 : Beta(2,3)
ssumnail3 : Beta(2,2)
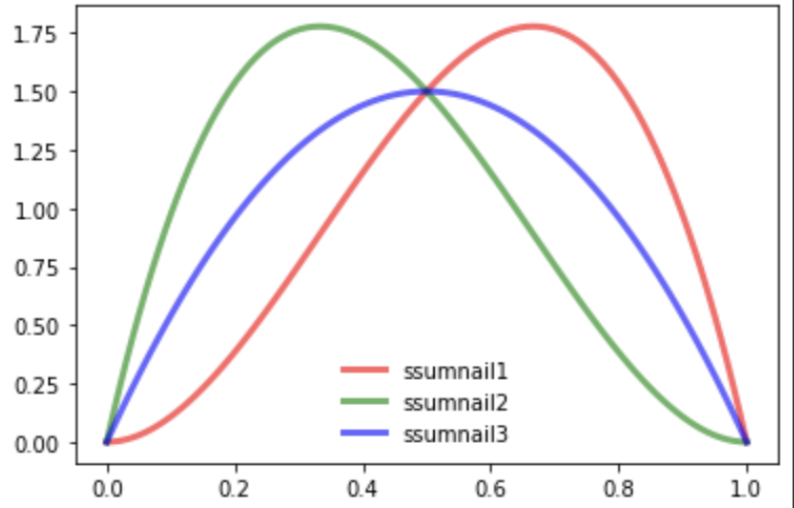
각 썸네일 별 클릭율:
ssumnail1 : 2/3 : 66%
ssumnail2 : 1/3: 33%
ssumnail3 : 1/2: 50%
이 상태에서 최고의 썸네일은 바로 1번이다. 그러나 Thompson Sampling은 다른 그리디 알고리즘처럼 1번을 택하지 않는다.
그 대신, 3개의 베타분포에서 임의의 점을 샘플링한다. 지금 그려진 그래프는 베타분포의 확률밀도함수이기 때문에 밑면의 넓이는 모두 1이고, 특정 x값에 해당하는 분포의 y값이 클수록 확률이 높다.(x축: 클릭 확률, y축: 클릭 확률에 대한 확률분포) 샘플링이란 밑면안에서의 임의의 점의 x좌표 추출을 의미한다.
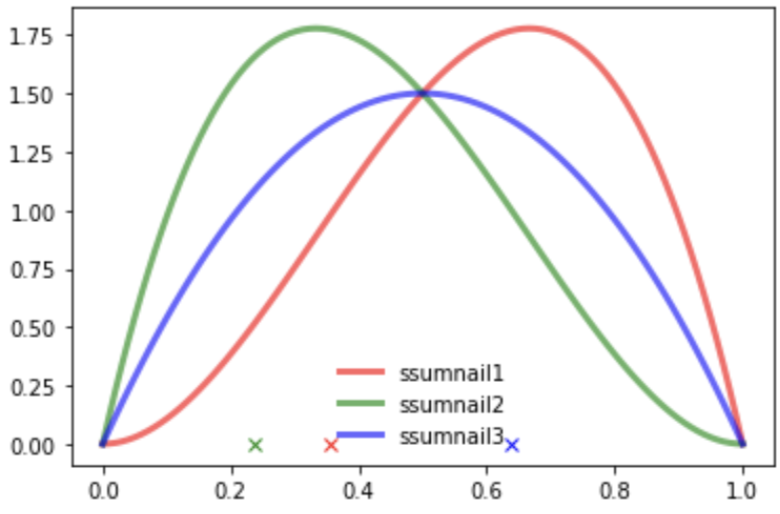
Thompson Sampling은 이렇게 샘플링한 점들 중에서 가장 샘플값이 큰 샘플을 배출한 썸네일을 고르게 된다. 고른 썸네일을 노출시키고 클릭 여부에 따라 파라미터를 재조정한다. 즉 위 사진에서는 썸네일3의 샘플값이 가장 크므로, 썸네일 3을 선택하게 된다. 그러나, 샘플링 횟수가 적을 때는 선택되는 썸네일이 매번 바뀐다. 여러번의 수행을 거쳐 확률밀도함수가 수렴하게 되면 비로소 확실한 썸네일이 선택되게 된다.
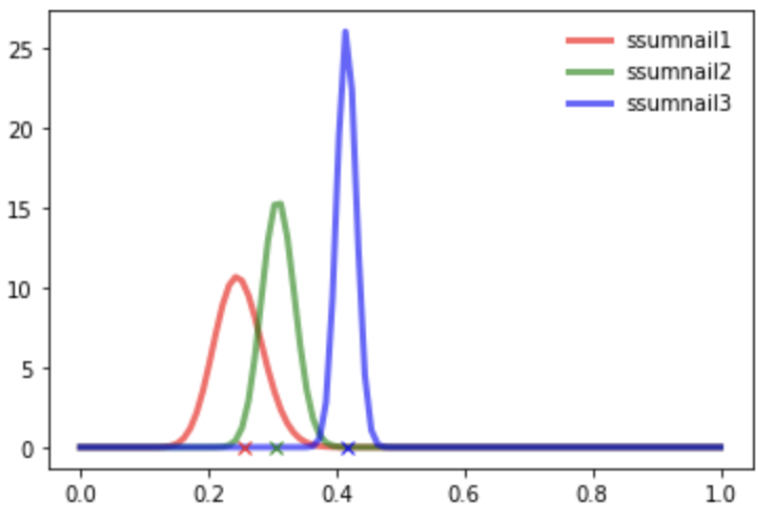
위 이미지처럼 수 많은 실험을 거치게 되면, 어떤 썸네일이 가장 반응이 좋은지가 명확하게 분포에서 표현이 된다.결국 썸네일3이 가장 우수하다는 것을 베이지안 추론을 통해 알 수 있게 된다.
위의 예시에서 보여준 Thompson Sampling 알고리즘의 과정을 다시 정리해보자.

1. K개의 Arm(예시:썸네일)을 노출시켰을 때의 성공(예시:클릭)확률에 대한 확률분포를 베타 분포로 보고 처음에는 베타 분포 전부 초기화
(예시에서는 S: 노출 후 클릭 횟수,F: 노출 후 클릭 안한 횟수, α,β =1)
2. 모든 i(예시에서는 썸네일 번호)에 대해 값을 샘플링(θ)한뒤, argmax를 이용해 가장 큰 샘플링값(θ)을 배출한 i찾기
3. 보상을 확인(예시에서는 클릭여부)하고 확인이 되었다면 S,F 값 재조정 후 Thompson Sampling 반복
마지막으로 MAB의 양대산맥인 UCB와 Thompson Sampling을 비교해보자.
UCB
-deterministic: 예측한 그대로 움직임(Qt,Nt)
-매 라운드(t 변할 때마다) 업데이트 필요(신뢰구간 설정 다시해야함)
Thompson Sampling
-probabilistic : 확률적으로 움직임
-늦게 들어오는 데이터 수용 가능(회원가입, 결제 데이터 등) : 노출시키고 반응을 살핀다.
-더 나은 경험적 증거
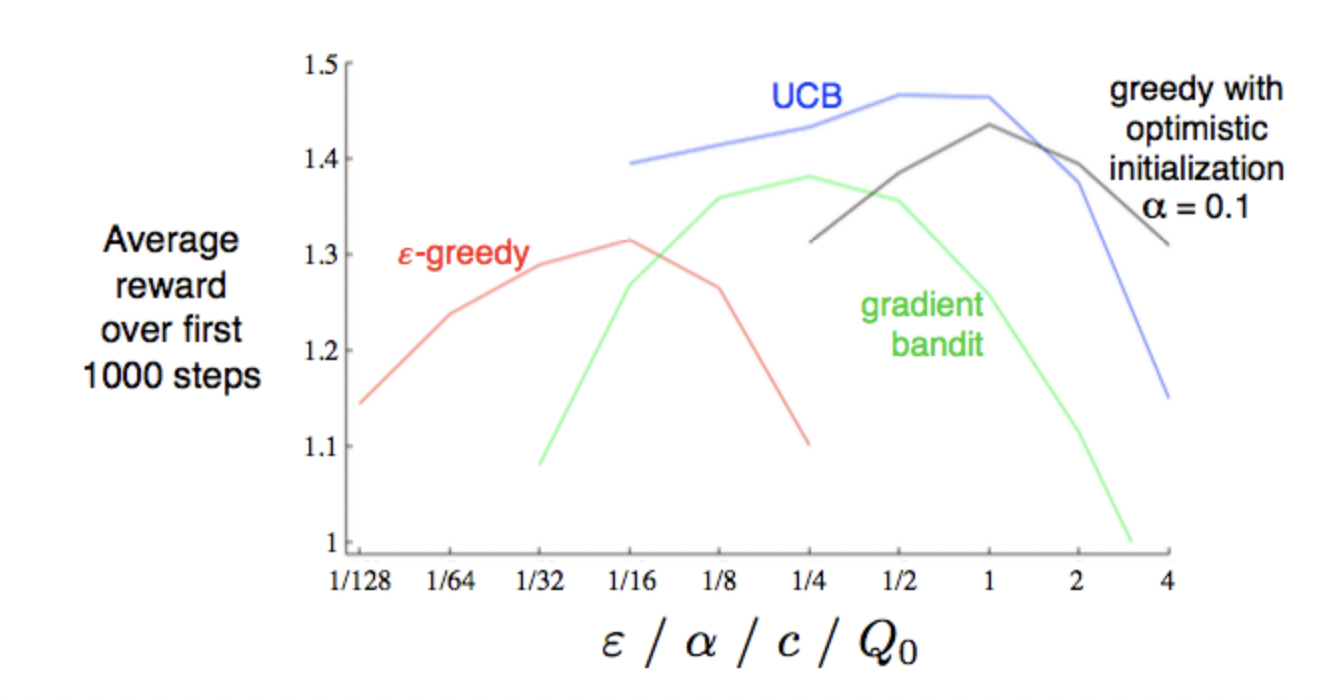
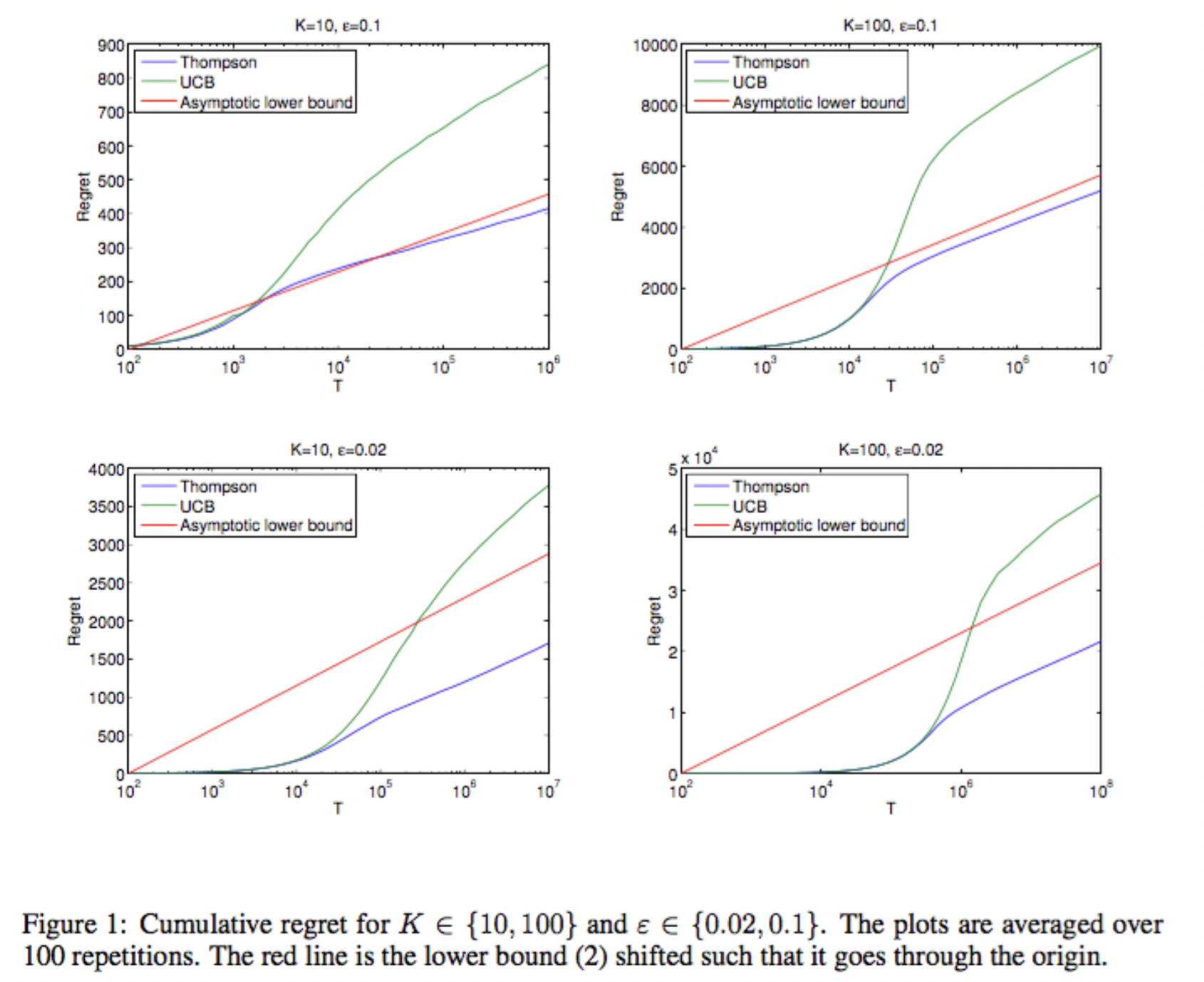
Thompson Sampling 논문을 보면, 아래 그래프에서는 UCB보다 좋은 성능을 보인다고 한다.
Y축의 Regret은 최선의 선택을 하지 않음에 따라 손해를 본 정도를 수치화 한것
참고문헌:
https://brunch.co.kr/@chris-song/66.
http://doc.mindscale.kr/km/data_mining/11.html
https://wonseokjung.github.io/RL-RL2/
https://soobarkbar.tistory.com/135
https://brunch.co.kr/@chris-song/62
https://m.blog.naver.com/nilsine11202/221912267111
멀티 암드 밴딧(Multi-Armed Bandits)
심플하고 직관적인 학습 알고리즘 | 강화학습의 정통 교과서라할 수 있는 Sutton 교수님의 Reinforcement Learning : An Introduction 책을 읽어보자. 챕터 1에서는 앞으로 다룰 내용에 대한 개요가 나오며, 챕
brunch.co.kr
MAB (Multi-Armed Bandits)
A / B Testing 의 단점을 보완 A / B Testing : A / B Testing URL A / B Testing이 단점을 간단히 얘기하면 다음과 같다. 테스트를 많이 하면 단기적으로 손해가 발생할 수 있다. A / B Testing의 결과는 시간의..
soobarkbar.tistory.com
제2편: 강화학습의 거의 모든것: Multi-armed Bandit
제1편: 강화학습의 거의 모든것 https://wonseokjung.github.io//reinforcementlearning/update/RL-RL1/ 제2편: 강화학습의 거의 모든것 : Multi-armed Bandit Multi-armed Bandit은 아주아주 간단한 Reinforcement 의 문제중 하나이
wonseokjung.github.io
http://doc.mindscale.kr/km/data_mining/11.html
11. A/B 테스팅과 '여러 팔 강도' 문제 11.1. A/B 테스팅 최근 인터넷을 이용한 상거래가 활발해지면서 'A/B 테스팅'이라는 아이디어가 인기를 얻게 되었다. A/B 테스팅은 메뉴, 문구, 광고 등을 고객마
doc.mindscale.kr
톰슨 샘플링 for Bandits
밴딧 문제를 해결하는 또 하나의 baseline | 이번 포스팅에서는 톰슨 샘플링에 대해 소개해드리겠습니다. 멀티암드밴딧(MAB) 보다는 좀 더 어려운 확률이론이 나오니, 먼저 대학교 때 기말고사를 보
brunch.co.kr




